
O perímetro do triângulo é o comprimento total do lado do triângulo. Portanto, a fórmula para o perímetro do triângulo é K = a + b + c ou a soma de todos os lados do triângulo.
Quando você circula em torno do jardim triangular, o que isso significa? Sim! Você está circulando em forma de triângulo. O que é uma forma de triângulo plano? A seguir está uma explicação do triângulo, o tipo de triângulo e como determinar ou a fórmula para o perímetro do triângulo.
Explicação do triângulo
Um triângulo é uma forma formada por três linhas que se cruzam e formam um ângulo. O número de ângulos em um triângulo é 180 graus.
Os triângulos são as formas planas mais simples porque são elementos que formam outras formas planas, como quadrados, retângulos, círculos e elementos de formas planas que formam formas como prismas e pirâmides.
Características de um Triângulo
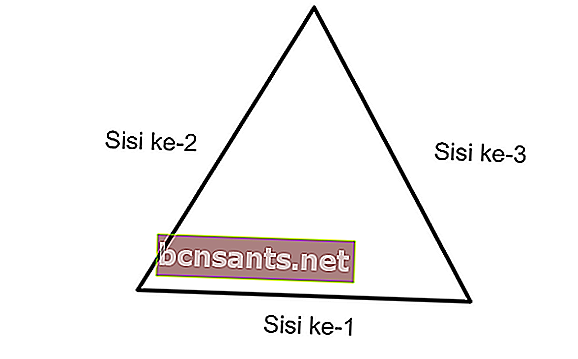
Para explicar melhor o significado de um triângulo, vou desenhar uma forma de triângulo ABC arbitrário da seguinte forma:
Os elementos do triângulo ABC incluem:
- Os pontos A, B e C são conhecidos como vértices.
- As linhas AB, BC e CA são chamadas de lados do triângulo.
- Os vários triângulos podem ser vistos a partir dos comprimentos laterais e dos ângulos formados pelo triângulo.
Tipos de Triângulos
Os tipos de triângulos variam amplamente com base no comprimento dos lados e ângulos que formam o triângulo. A seguir está a divisão dos tipos de triângulos
Tipos de triângulos baseados em comprimentos laterais
- Triângulo Equilátero
Ou seja, um triângulo com todos os três lados do mesmo comprimento. Além disso, os três ângulos formados pelo triângulo lateral têm o mesmo tamanho, que é 60 graus, porque o número de ângulos do triângulo é 180 graus.
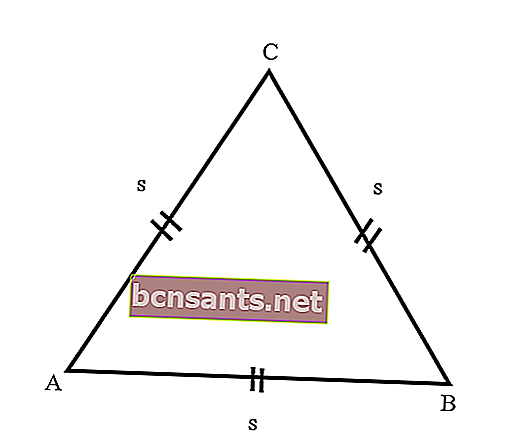
Para saber mais sobre os triângulos equiláteros, considere a seguinte explicação das propriedades dos triângulos equiláteros:

Na Figura (b) - (d), parece que a forma do triângulo ABC pode ocupar seu quadro exatamente usando 3 maneiras, a saber, girado até 120 graus centrado no ponto O (observe a direção de rotação) na (Figura b) girado até 240 graus no centro de rotação em O (na figura c) que é girado 360 graus (uma volta completa) no ponto central em O (na figura d).
Leia também: Fórmulas de oportunidade e exemplos de problemasDe acordo com a explicação das figuras a a f, o triângulo equilátero ABC tem simetria rotacional até o nível 3. Enquanto isso, as figuras e, f e g que estão invertidas podem ocupar o quadro corretamente. Para isso, o formato do triângulo ABC possui 3 eixos de simetria. Enquanto na imagem acima, os eixos de simetria são CD, BF e AE. Para que o triângulo equilátero possa ocupar o quadro de exatamente 6 maneiras.
Com base em algumas das descrições acima, algumas das propriedades que existem em um triângulo equilátero incluem: ele tem 3 níveis de simetria rotacional, 3 eixos de simetria, 3 lados equiláteros, 3 ângulos iguais de 60 graus e pode ocupar o quadro de até 6 maneiras.
- Triângulo isósceles
Ou seja, um triângulo com um lado do mesmo comprimento. Um triângulo isósceles tem dois ângulos iguais, ou seja, ângulos voltados um para o outro.
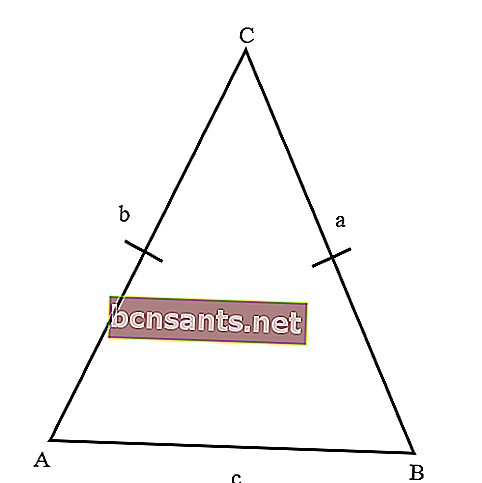
A seguir estão as propriedades do triângulo isósceles;
- Construindo um triângulo isósceles, girando-o por uma volta completa, ele ocupa o quadro exatamente de uma maneira. De forma que o triângulo samakaki tem uma simetria rotativa de um.
- Enquanto isso, um triângulo isósceles tem apenas um eixo de simetria.
- Qualquer triângulo
Ou seja, um triângulo com três lados que não são do mesmo comprimento e os três ângulos não são iguais.

Aqui estão as propriedades de qualquer triângulo:
- Tem três lados que não têm o mesmo comprimento. (Na imagem acima, os três lados significados são o comprimento de BA ≠ CB ≠ AC).
- Não tem simetria de dobra.
- Possui apenas uma simetria rotativa.
- Os três cantos têm tamanhos diferentes.
Tipos de triângulos baseados no ângulo
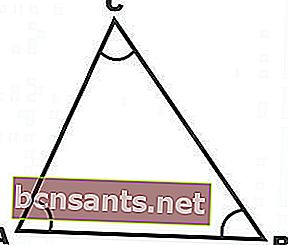
- Triângulo agudo
Ou seja, um triângulo com todos os três ângulos formando um ângulo agudo. Um ângulo agudo é um ângulo que varia de 0 a 90 graus.
- Triângulo cego
Ou seja, um triângulo com um canto formando um ângulo obtuso. Um ângulo obtuso é um ângulo cuja magnitude está na faixa de 90 a 180 graus.
Leia também: Soluções para fórmulas frequentemente esquecidas!
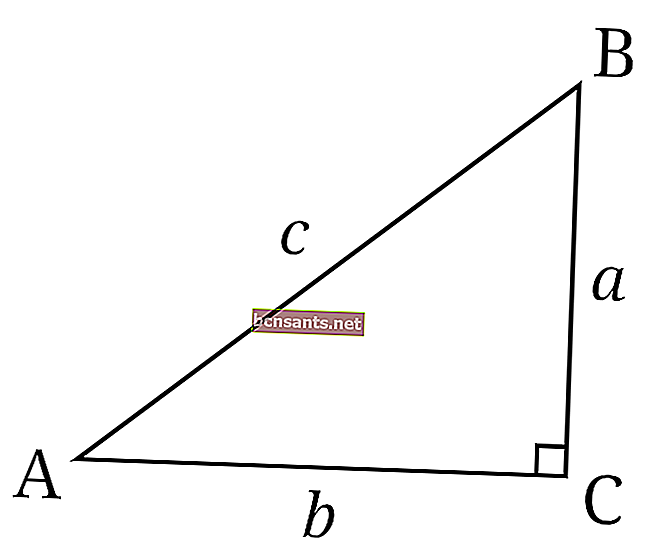
- Triângulo retângulo
Ou seja, um triângulo com um dos cantos formando um ângulo de 90 graus.
A fórmula para o perímetro de um triângulo
O perímetro da forma é obtido a partir do número de comprimentos das arestas (sisis) que formam a forma.
Portanto, a fórmula para o perímetro de um triângulo pode ser obtida somando cada lado do triângulo.
Perímetro do triângulo = comprimento do 1º lado + comprimento do 2º lado + comprimento do 3º lado
K = a + b + c
Exemplo de problema para encontrar o perímetro de um triângulo
Problema de exemplo 1.
Um triângulo equilátero tem um comprimento lateral de 3 cm, qual é a circunferência!
Solução:
Você sabe: s = 3 cm
Procura-se: perímetro do triângulo?
Responda:
Os triângulos equilaterais têm os mesmos lados,
K = s + s + s
K = 3 + 3 + 3
K = 9 cm
Portanto, o perímetro do triângulo equilátero é de 9 cm.
Exemplo de problema 2.
Um triângulo isósceles tem um comprimento lateral total de 36 cm. O lado mais comprido tem 13 cm. Qual é o comprimento do lado mais curto?
Solução:
Você sabe que = K = 36 cm; b = a = 13 cm
Procura-se : o comprimento do lado mais curto?
Resposta :
Perímetro do triângulo = a + b + c
36 = 13 + 13 + c
c = 10 cm
Então, o menor comprimento do lado do triângulo é de 10 cm
Exemplo de problema 3.
Você tem um triângulo arbitrário com lados de 9, 11, 13 cm cada. Calcule o perímetro do triângulo!
Solução:
Sabe-se que : a = 13 cm; b = 9 cm; c = 11cm
Procura-se : perímetro do triângulo?
Responda:
K = a + b + c
K = 13 +9 +11
K = 33 cm
Então, o perímetro do triângulo é de 33 cm
Exemplo de problema 4.
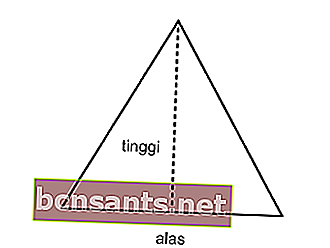
Calcule o perímetro do triângulo isósceles com área de 12 cm2 e comprimento lateral de 6 cm!
Solução:
Você sabe: L = 12 cm2; a = 6 cm
Procura-se: perímetro do triângulo?
Responda:
Para encontrar o perímetro do triângulo, você deve saber o comprimento dos lados do triângulo.
Use a área para encontrar a altura do triângulo
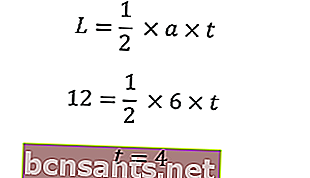
Usando o sistema pitagórico, conhecemos a hipotenusa de um triângulo isósceles inserindo o comprimento da base (a) e a altura do triângulo (t)

Usando a equação acima, obtemos a hipotenusa do triângulo
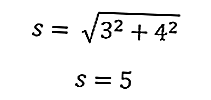
Isso permitirá que você calcule o perímetro do triângulo imediatamente
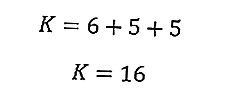
Então, o perímetro do triângulo é de 16 cm
Referência : Triangle - Math is Fun
