
A fórmula pitagórica é a fórmula usada para encontrar um dos comprimentos laterais de um triângulo.
A fórmula pitagórica, também conhecida como teorema de Pitágoras, é uma das primeiras matérias de matemática ensinadas.
Desde o ensino fundamental, aprendemos essa fórmula pitagórica.
Neste artigo, discutirei novamente a proposição do teorema de Pitágoras, juntamente com exemplos de problemas e suas soluções.
História de Pitágoras - Pitágoras
Na verdade, Pitágoras é o nome de uma pessoa dos tempos da Grécia Antiga em 570-495 AC.
Pitágoras foi um brilhante filósofo e cientista matemático de sua época. Isso é evidenciado por suas descobertas, que conseguiram resolver o problema do comprimento lateral do triângulo com uma fórmula muito simples.
Teorema de Pitágoras
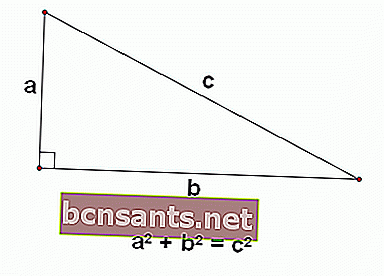
O Teorema de Pitágoras é uma proposição matemática sobre triângulos retângulos, que mostra que o comprimento da base do quadrado mais o comprimento da altura do quadrado é igual ao comprimento da hipotenusa do quadrado.
Suponha ...
- O comprimento da base do triângulo é um
- O comprimento da altura é b
- O comprimento da hipotenusa é c
Assim, usando o argumento de Pytaghoras, a relação entre os três pode ser formulada para ser
a 2 + b 2 = c 2
Prova do Teorema de Pitágoras
Se você for observador, poderá imaginar que basicamente a fórmula de pytaghoras mostra que a área de um quadrado com lado a mais a área de um quadrado com lado b é igual à área de um quadrado com lado c.
Você pode ver a ilustração na imagem a seguir:

Você também pode assistir em um vídeo como o seguinte
Como usar a fórmula pitagórica
A fórmula do fitágoras a 2 + b 2 = c 2 pode ser expressa basicamente de várias formas, a saber:
a2 + b2 = c2
c2 = a 2 + b 2
a2 = c2 - b 2
b2 = c2 -a2
Para resolver cada uma dessas fórmulas, você pode usar o valor da raiz da fórmula pitagórica acima.
Leia também: Microscópio: Explicação, suas partes e função
Observação importante: não se esqueça de que as fórmulas acima se aplicam apenas a triângulos retângulos. Se não, não é válido.
Pitágoras triplo (padrão numérico)
Triplo pitagórico é o nome do padrão de número abc que atende à fórmula pitagórica acima.
São tantos os números que preenchem essas pytaghoras triplas, até mesmo números muito grandes.
Alguns exemplos incluem:
- 3 - 4 - 5
- 5 - 12 - 13
- 6 - 8 - 10
- 7 - 24 - 25
- 8 a 15 a 17
- 9-12-15
- 10 - 24 - 26
- 12 - 16 - 20
- 14 - 48 - 50
- 15 - 20 - 25
- 15 - 36 - 39
- 16-30-34
- 17 - 144 - 145
- 19 - 180 - 181
- 20 - 21 - 29
- 20 - 99 - 101
- 21 - 220 - 221
- 23 - 264 - 265
- 24 –143 - 145
- 25 - 312 - 313
- etc
A lista ainda pode ser continuada para um número muito grande.
Em essência, os números corresponderão quando você inserir os valores na fórmula a 2 + b 2 = c 2
Exemplos de perguntas completas e discussão
Para entender melhor o tópico desta fórmula de Pytaghoras, vamos olhar o exemplo da pergunta completa e sua discussão abaixo.
Exemplo de fórmula pitagórica 1
1. Um triângulo tem o lado BC de 6 cm de comprimento e o lado AC de 8 cm , quantos cm tem a hipotenusa do triângulo (AB)?
Solução:
Conhecido:
- BC = 6 cm
- AC = 8 cm
Desejado: comprimento AB?
Responda:
AB2 = BC2 + AC2
= 62 + 82
= 36 + 64
= 100
AB = √100
= 10
Assim, o comprimento do lado AB (inclinação) é de 10 cm.
Exemplo de Teorema de Pitágoras 2
2. Sabe-se que um triângulo tem uma hipotenusa de 25 cm de comprimento e o lado vertical do triângulo tem 20 cm de comprimento . Qual é o comprimento do lado plano?
Solução:
É sabido: fazemos um exemplo, para tornar mais fácil
- c = hipotenusa, b = lado plano, a = lado vertical
- c = 25 cm, a = 20 cm
Desejado: O comprimento do lado plano (b)?
Responda:
b2 = c2 - a2
= 252 - 202
= 625 - 400
= 225
b = √225
= 15 cm
Para que o comprimento do lado plano do triângulo seja de 15 cm .
Exemplo de Fórmula Pitagórica 3
3. Qual é o comprimento do lado vertical de um triângulo se sabemos que a hipotenusa do triângulo tem 20 cm e o lado plano tem 16 cm .
Solução :
É sabido: primeiro fazemos o exemplo e o valor
- c = hipotenusa, b = lado plano, a = lado vertical
- c = 20 cm , b = 16 cm
Desejado: O comprimento da vertical (a)?
Responda:
a2 = c2 - b2
= 202 - 162
= 400 - 256
= 144
a = √144
= 12 cm
A partir disso, você obtém o comprimento do lado do triângulo que está em pé é de 12 cm .
Exemplo de Triplo Pitágoras Problema 4
Continue o valor do seguinte triplo pitagórico….
3, 4,….
6, 8,….
5, 12,….
Solução:
Assim como as soluções dos problemas anteriores, esta relação tripla pitagórica pode ser resolvida usando a fórmula c2 = a 2 + b 2.
Por favor, tente calcular você mesmo….
A resposta (a ser correspondida) é:
- 5
- 10
- 13
Exemplo de Fórmulas Pitagóricas - Problema 5
Dado que três cidades (A, B, C) formam um triângulo, com cotovelos na cidade B.
Distância para a cidade AB = 6 km, distância para a cidade BC = 8 km, qual é a distância para a cidade AC?
Solução:
Você pode usar a fórmula do teorema de Pitágoras e obter o resultado do cálculo da distância da cidade AC = 10 km.
Daí a discussão da fórmula pitagórica - os argumentos do teorema de Pitágoras, que é apresentado de forma simples. Espero que você possa entendê-lo bem, para que mais tarde possa entender outros tópicos de matemática, como trigonometria, logaritmos e assim por diante.
Se ainda tiver dúvidas, você pode enviá-las diretamente na coluna de comentários.
Referência
- Qual é a proposição de Pitágoras? - perguntando filho
- Teorema de Pitágoras - Matemática é divertida
