
A equação quadrática é uma das equações matemáticas da variável que tem a maior potência de dois.
A forma geral de uma equação quadrática ou PK é a seguinte:
machado 2 + bx + c = 0
onde x é a variável, a , b é o coeficiente e c é a constante. O valor de a não é igual a zero.
Formas de gráfico
Se uma equação quadrática for descrita em termos de coordenadas cartesianas (x, y), ela formará um gráfico parabólico. Portanto, as equações quadráticas também são freqüentemente chamadas de equações parabólicas .
O seguinte é um exemplo da forma desta equação na forma de um gráfico parabólico.
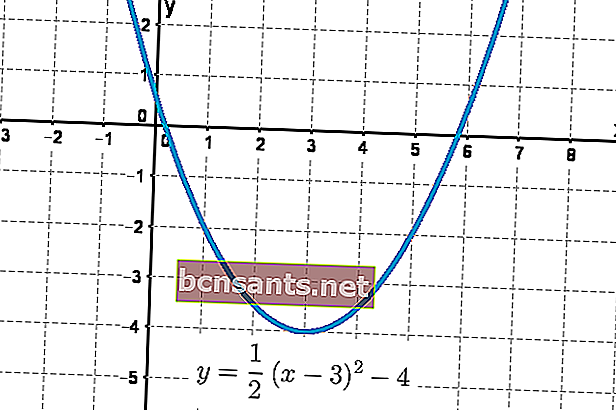
Na equação geral, os valores a , b e c influenciam muito o padrão parabólico resultante.
O valor de a determina a curva côncava ou convexa da parábola. Se o valor de a> 0, a parábola se abrirá (côncava) . Por outro lado, se a <0 , a parábola se abrirá para baixo (convexa) .

O valor de b na equação determina o vértice da parábola . Em outras palavras, determine o valor do eixo da simetria da curva que é igual ax = - b / 2a .

O valor constante c no gráfico da equação determina o ponto de intersecção da função de parábola no eixo y . O seguinte é um gráfico parabólico com mudanças no valor constante c .

Raízes da Equação Quadrática (PK)
A solução para uma equação quadrática é chamada de kar - a raiz da equação quadrática .
Várias Raízes PK
Os tipos de raízes PK podem ser encontrados facilmente usando a fórmula geral D = b2 - 4ac da equação geral para o quadrático ax2 + bx + c = 0.
A seguir estão os tipos de raízes de equações quadráticas.
1. Raiz real (D> 0)
Se o valor de D> 0 de um PK, ele produzirá raízes reais, mas terá raízes diferentes. Em outras palavras, x1 não é o mesmo que x2.
Exemplo da equação da raiz real (D> 0)
Encontre o tipo de raiz da equação x2 + 4x + 2 = 0.
Solução:
a = 1; b = 4; e c = 2
D = b2 - 4ac
D = 42 - 4 (1) (2)
D = 16 - 8
D = 8
Portanto, como o valor de D> 0, a raiz é do tipo raiz real.
2. Raiz real é igual a x1 = x2 (D = 0)
É um tipo de raiz de uma equação quadrática que produz raízes com o mesmo valor (x1 = x2).
Exemplo de raízes reais (D = 0)
Encontre o valor da raiz PK de 2x2 + 4x + 2 = 0.
Leia também: Tipos de Ciclos de Água (+ Imagem Completa e Explicação)Solução:
a = 2; b = 4; c = 2
D = b2 - 4ac
D = 42 - 4 (2) (2)
D = 16 - 16
D = 0
Portanto, como o valor de D = 0, fica comprovado que as raízes são reais e geminadas.
3. Raízes imaginárias / não reais (D <0)
Se o valor de D <0, a raiz da equação quadrática será imaginária / não real.
Exemplo de raízes imaginárias (D <0) /
Encontre o tipo de raiz da equação x2 + 2x + 4 = 0.
Solução:
a = 1; b = 2; c = 4
D = b2 - 4ac
D = 22 - 4 (1) (4)
D = 4 - 16
D = -12
Portanto, como o valor de D <0, a raiz da equação é uma raiz irreal ou imaginária.
Encontre as raízes da equação quadrática
Existem vários métodos que podem ser usados para encontrar as raízes de uma equação quadrática. Entre eles estão a fatoração, quadrados perfeitos e o uso da fórmula abc.
O seguinte descreve vários métodos para encontrar raízes de equação.
1. Fatoração
Fatoração / fatoração é um método de encontrar raízes procurando um valor que, se multiplicado, produzirá outro valor.
Existem três formas de equações quadráticas (PK) com fatoração de raiz diferente, a saber:
| Não. | Forma de equação | Fatoração Root-Root |
| 1 | x 2 + 2xy + y 2 = 0 | (x + y) 2 = 0 |
| 2 | x 2 - 2xy + y 2 = 0 | (x - y) 2 = 0 |
| 3 | x 2 - y 2 = 0 | (x + y) (x - y) = 0 |
A seguir está um exemplo de um problema sobre o uso do método de fatoração em equações quadráticas.
Resolva a equação quadrática 5x 2 + 13x + 6 = 0 usando o método de fatoração.
Solução:
5x2 + 13x = 6 = 0
5x2 + 10x + 3x + 6 = 0
5x (x + 2) + 3 (x + 2) = 0
(5x + 3) (x + 2) = 0
5x = -3 ou x = -2
Então, a solução é x = -3/5 ou x = -2
2. Quadrados perfeitos
A forma quadrática perfeita é uma equação quadrática que produz números racionais .
Os resultados de uma equação quadrática perfeita geralmente usam a seguinte fórmula:
(x + p) 2 = x2 + 2px + p2
A solução geral para a equação quadrática perfeita é a seguinte:
(x + p) 2 = x2 + 2px + p2
com (x + p) 2 = q, então:
(x + p) 2 = q
x + p = ± q
x = -p ± q
A seguir está um exemplo de um problema sobre o uso do método de equação perfeita.
Resolva a equação x2 + 6x + 5 = 0 usando o método da equação quadrática perfeita!
Solução:
x2 + 6x +5 = 0
x2 + 6x = -5
A próxima etapa é adicionar um número nos lados direito e esquerdo para que possa mudar para um quadrado perfeito.
x2 + 6x + 9 = -5 + 9
x2 + 6x + 9 = 4
(x + 3) 2 = 4
(x + 3) = √4
x = 3 ± 2
Então, o resultado final é x = -1 ou x = -5
Leia também: Definição e diferença de homônimos, homófonos e homógrafos3. Fórmulas Quadráticas ABC
A fórmula abc é uma escolha alternativa quando a equação quadrática não pode ser resolvida por fatoração ou métodos quadráticos perfeitos.
A seguir está a fórmula abc para a equação quadrática ax2 + bx + c = 0.
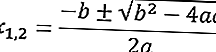
A seguir está um exemplo de solução de um problema de equação quadrática usando a fórmula abc .
Resolva a equação x2 + 4x - 12 = 0 usando o método da fórmula abc!
Solução:
x2 + 4x - 12 = 0
onde a = 1, b = 4, c = -12

Construindo uma nova equação quadrática
Se aprendemos anteriormente como encontrar as raízes da equação, agora aprenderemos a compor a equação quadrática a partir das raízes conhecidas anteriormente.
Aqui estão algumas maneiras de construir um novo PK.
1. Construir equações quando as raízes forem conhecidas
Se uma equação tem raízes x1 e x2, então a equação para essas raízes pode ser expressa em termos de
(x- x 1 ) (x- x 2 ) = 0
Exemplo:
Encontre uma equação quadrática onde as raízes estão entre -2 e 3.
Solução:
x 1 = -2 e x 2 = 3
(x - (- 2)) (x-3) = 0
(x + 2) (x + 3)
x2-3x + 2x-6 = 0
x2-x-6 = 0
Então, o resultado da equação para essas raízes é x2-x-6 = 0
2. Construa uma equação quadrática se você souber o número e o produto das raízes
Se as raízes da equação quadrática com o número e as vezes x1 e x2 forem conhecidas, a equação quadrática pode ser convertida na seguinte forma.
x2- (x 1+ x 2 ) x + (x 1. x 2 ) = 0
Exemplo:
Encontre uma equação quadrática com raízes 3 e 1/2.
Solução:
x 1 = 3 e x 2 = -1/2
x 1+ x 2 = 3 -1/2 = 6/2 - 1/2 = 5/2
x 1. x 2 = 3 (-1/2) = -3/2
Assim, a equação quadrática é:
x2- (x 1+ x 2 ) x + (x 1. x 2 ) = 0
x2– 5/2 x - 3/2 = 0 (cada lado multiplicado por 2)
2x2-5x-3 = 0
Portanto, a equação quadrática para as raízes 3 e 1/2 é 2x2-5x-3 = 0.
