
A equação para um círculo tem a forma geral x ^ 2 + y ^ 2 + Ax + By + C = 0, que pode ser usada para determinar o raio e o centro de um círculo.
A Equação de Círculo que você aprenderá a seguir tem várias formas. Em casos diferentes, a equação pode ser diferente. Portanto, compreenda-o bem para que você possa memorizá-lo de cor.
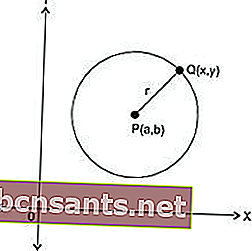
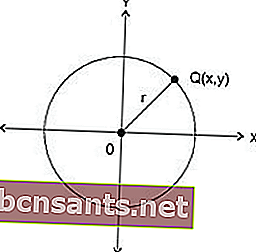
Círculo é um conjunto de pontos equidistantes de um ponto. As coordenadas desses pontos são determinadas pelo arranjo das equações. Isso é determinado com base no comprimento do raio e nas coordenadas do centro do círculo.
Equações do Círculo
Existem vários tipos de equações, nomeadamente equações formadas a partir do ponto central e raio e uma equação que pode ser encontrada para o ponto central e raio.
Equação de círculo geral
Existe uma equação geral, conforme abaixo:
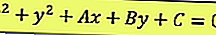
A julgar pela equação acima, o ponto central e o raio podem ser determinados, são:
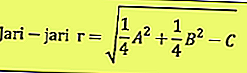
O centro do círculo é:
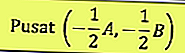
No centro de P (a, b) e raio r
De um círculo, se você souber o ponto central e o raio, obterá a fórmula:
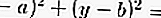
Se você souber o ponto central de um círculo e o raio do círculo, onde (a, b) é o centro e r é o raio do círculo.
A partir da equação obtida acima, podemos determinar se a inclusão do ponto está localizada no círculo, ou dentro ou fora. Para determinar a localização do ponto, usando a substituição do ponto nas variáveis xey e depois comparando os resultados com o quadrado do raio do círculo.
Um ponto M (x 1 , y 1 ) reside:
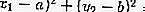
No círculo:
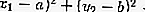
Dentro do círculo:
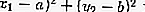
Fora do círculo:
Com centro O (0,0) e raio r
Se o ponto central estiver em O (0,0), faça a substituição da parte anterior, a saber:
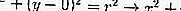
A partir da equação acima, pode-se determinar a localização de um ponto no círculo.
Um ponto M (x 1 , y 1 ) reside:
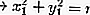
No círculo:
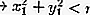
Dentro do círculo:
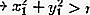
Fora do círculo: Leia também: Arte é: Definição, Função, Tipos e Exemplos [COMPLETO]
A forma geral da equação pode ser expressa nas seguintes formas.
(x - a) 2 + (y - b) 2 = r2, ou
X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0, ou
X2 + y2 + Px + Qy + S = 0, onde P = -2a, Q = -2b e S = a2 + b2 - r2
A Intersecção de Linhas e Círculos
Um círculo com a equação x2 + y2 + Ax + By + C = 0 pode ser determinado se uma linha h com a equação y = mx + n não a toca, ofende ou intercepta usando o princípio discriminante.
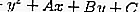
……. (equação 1)
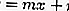
…… .. (equação 2)
Ao substituir a equação 2 na equação 1, você obterá uma equação quadrática, a saber:
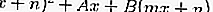
A partir da equação quadrática acima, ao comparar os valores discriminantes, pode-se ver se a linha não ofende / corta, ofende ou intercepta o círculo.
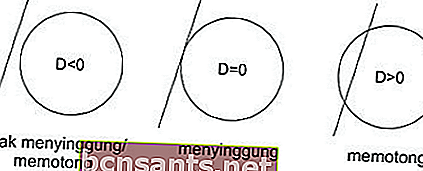
A linha h não intercepta / ofende o círculo, então D <0
A linha h é tangente ao círculo, então D = 0
A linha h cruza o círculo, então D> 0
Equações de tangentes a círculos
1. Equação de tangentes através de um ponto em um círculo
Tangentes a um círculo encontram exatamente um ponto localizado no círculo. A partir do ponto de intersecção da tangente e do círculo, a equação da reta da tangente pode ser determinada.
A equação para a tangente ao círculo através do ponto P (x 1 , y 1 ), pode ser determinada, a saber:
- Forma
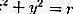
A equação da tangente
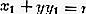
- Forma
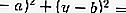
A equação da tangente
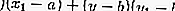
- Forma
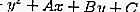
A equação da tangente
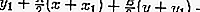
Exemplo de problemas:
A equação para a tangente através do ponto (-1,1) no círculo
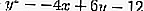
estão:
Responda:
Conheça a equação do círculo
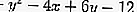
onde A = -4, B = 6 e C = -12 e x 1 = -1, y 1 = 1
PGS é
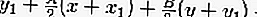
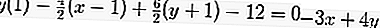
Portanto, a equação da tangente é
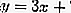
2. A equação tangencia o gradiente
Se uma linha com inclinação m é tangente a um círculo,
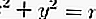
então a equação da tangente é:
Se é um círculo,
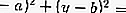
então a equação da tangente:

Se é um círculo,
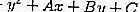
então a equação da tangente substituindo r por,
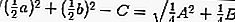
de modo a:
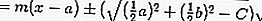
ou
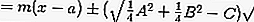
3. Equações de tangentes para pontos fora do círculo
De um ponto fora do círculo, duas tangentes ao círculo podem ser desenhadas.
Leia também: Democracia: Definição, História e Tipos [COMPLETO]Para encontrar a equação tangente, a fórmula da equação da linha regular é usada, a saber:
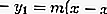
Porém, a partir desta fórmula, o valor da inclinação da linha é desconhecido. Para encontrar a inclinação da linha, substitua a equação do círculo pela equação. Como a linha é uma tangente, então a partir da equação resulta a substituição para o valor D = 0, e o valor de m será obtido
Exemplo de problemas
Exemplo de problema 1
Um círculo tem um ponto central (2, 3) e 8 cm de diâmetro. A equação do círculo é ...
Discussão:
Porque d = 8 significa r = 8/2 = 4, então a equação para o círculo que é formado é
(x - 2) ² + (y - 3) ² = 42
x² - 4x + 4 + y² -6y + 9 = 16
x² + y² - 4x - 6y - 3 = 0
Exemplo de problema 2
Encontre a equação geral para o círculo centrado no ponto (5,1) e ofendendo a linha 3 x - 4 y + 4 = 0!
Discussão:
Se for conhecido que o centro do círculo ( a , b ) = (5,1) e a tangente ao círculo é 3 x - 4 y + 4 = 0, então o raio do círculo é formulado da seguinte maneira.
Assim, a equação geral para o círculo é a seguinte.
Assim, a equação geral para um círculo centrado em (5,1) e violando a linha 3 x - 4 y + 4 = 0 é
Exemplo de problema 3
Encontre a equação geral para um círculo centrado em (-3,4) e violando o eixo Y!
Discussão:
Em primeiro lugar, vamos desenhar o gráfico do círculo primeiro, que está centrado em (-3,4) e prejudicando o eixo Y!
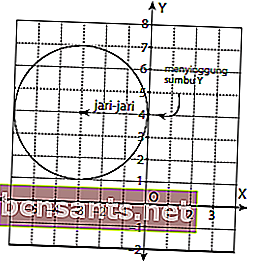
Com base na imagem acima, pode-se observar que o centro do círculo está na coordenada (-3,4) com raio 3, de forma que:
Assim, a equação geral que está centrada em (-3,4) e ofende o eixo Y é
Em alguns casos, o raio do círculo não é conhecido, mas a tangente é conhecida. Então, como determinar o raio do círculo? Veja a seguinte imagem.
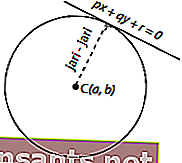
A imagem acima mostra que a tangente à equação px + qy + r = 0 pertence ao círculo centrado em C ( a, b ). O raio pode ser determinado pela seguinte equação. a, b ). O raio pode ser determinado pela seguinte equação.

Pode ser útil.
