Tabela trigonométrica Sin Cos Tan completa (todos os ângulos) + Como entendê-la

A tabela trigonométrica sen cos tan é uma série de tabelas que contém o valor trigonométrico ou sen cos tangente de um ângulo.

Neste artigo, uma tabela de valores trigonométricos para sin cos tan é mostrada de vários ângulos especiais do ângulo 0º a 360º (ou o que é comumente chamado de ângulo de círculo de 360 ​​graus), para que você não precise se preocupar mais em memorizá-los.

Quanto à fórmula de identidade trigonométrica, você pode lê-la neste artigo.

Definição de Sin Cos Tan

Antes de entrar na tabela de valores trigonométricos, é uma boa ideia primeiro entender os termos trigonometria e sin cos tan.

• A trigonometria é um ramo da matemática que estuda a relação entre o comprimento e o ângulo de um triângulo.
• Sin (seno) é a razão do comprimento em um triângulo entre a frente do ângulo e a hipotenusa, y / z.
• Cos (cosseno) é a razão do comprimento em um triângulo entre o lado do ângulo e a hipotenusa, x / z.
• Tan (tangente) é a proporção dos comprimentos em um triângulo entre a frente do canto e o lado, y / x.

Todas as comparações trigonométricas de tan sin cos são limitadas a apenas triângulos retângulos válidos ou triângulos com um ângulo de 90 graus.

Quadrante I Tabela de trigonometria de ângulo especial (0 - 90 graus)

Canto	0 º	30 º	45 º	60 º	90 º
Pecado	0	1/2	1/2 √2	1/2 √3	1
Cos	1	1/2 √3	1/2 √2	1/2	0
bronzeado	0	1/2 √3	1	√3	∞

Tabela de trigonometria do quadrante de ângulo especial II (90 - 180 graus)

Canto	90 º	120 º	135 º	150 º	180 º
Pecado	1	1/2 √3	1/2 √2	1/2	0
Cos	0	- 1/2	- 1/2 √2	- 1/2 √3	-1
bronzeado	∞	-√3	-1	- 1/3 √3	0

Mesa Sin Cos Tan Quadrante de ângulo especial III (180 - 270 graus)

Canto	180 º	210 º	225 º	240 º	270 º
Pecado	0	- 1/2	- 1/2 √2	- 1 / 2√3	-1
Cos	-1	- 1 / 2√3	- 1 / 2√2	- 1/2	0
bronzeado	0	1 / 3√3	1	√3	∞

Mesa Cos Sin Tan Quadrante de ângulo especial IV (270 - 360 graus)

Canto	270 º	300 º	315 º	330 º	360 º
Pecado	-1	-½√3	-½√2	-½	0
Cos	0	½	½√2	½√3	1
bronzeado	∞	-√3	-1	-1 / 3√3	0

Esta é uma lista completa de tabelas trigonométricas de todos os ângulos especiais de 0 a 360 graus.

Leia também: Processo do mecanismo de visão humana e dicas de cuidados com os olhos

Você pode usar esta tabela para facilitar os negócios no cálculo ou análise de trigonometria em matemática.

Relembrando a Tabela Trigonométrica de Ângulos Especiais sem Memorização

Na verdade, você não precisa se preocupar em memorizar todos os valores trigonométricos de todos os ângulos.

Tudo que você precisa é um conceito básico de compreensão que possa usar para descobrir o valor trigonométrico de qualquer ângulo específico.

Você só precisa se lembrar dos componentes do comprimento lateral do triângulo nos ângulos especiais 0, 30, 45, 60 e 90 graus.

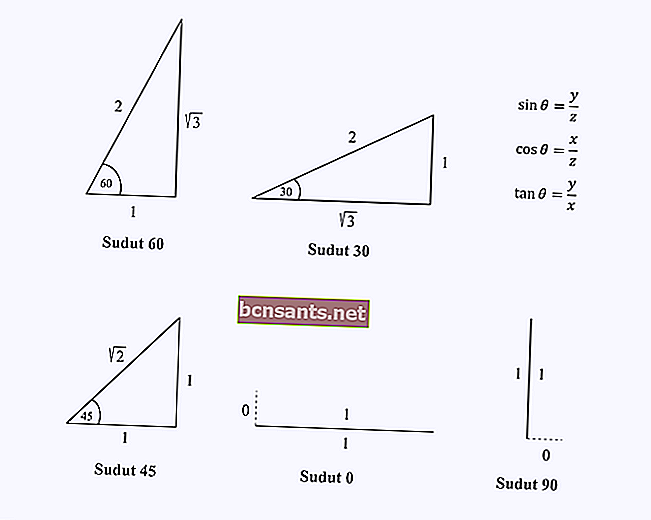
Suponha que você queira encontrar o valor de cos (60).

Você só precisa lembrar o comprimento do lado do triângulo com um ângulo de 60 graus e, em seguida, realizar a operação do cosseno, que é x / z nesse triângulo.

Na figura, você verá que o valor para cos 60 = 1/2.

Fácil, certo?

Para os ângulos nos outros quadrantes, o método é o mesmo e você só precisa ajustar o sinal positivo ou negativo de cada quadrante.

Mesa em forma de círculo

Se a tabela de cos sen tan acima for muito longa para lembrar, também se o método de conceito de ângulo especial que você acha que ainda é difícil ...

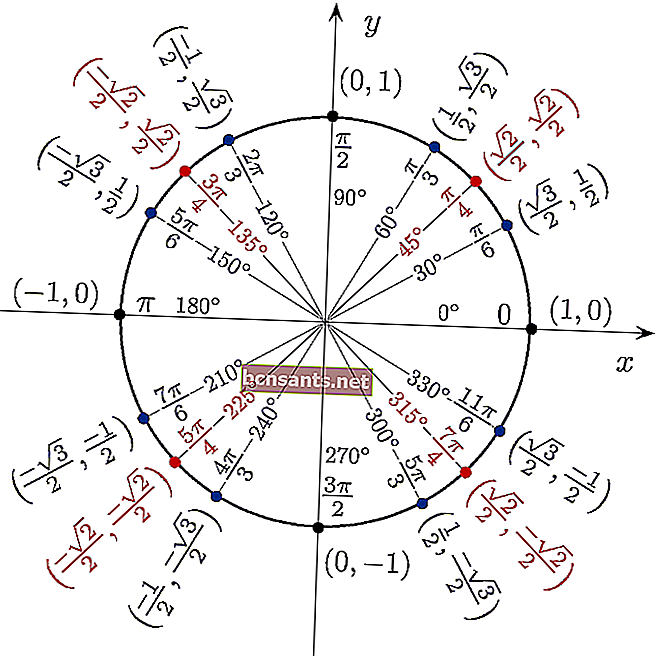
Você pode usar a tabela trigonométrica na forma de um círculo para ver diretamente o valor de sen cos tan de um ângulo de 360 ​​graus.

Truques rápidos para memorizar tabelas trigonométricas

Além dos métodos acima, ainda há mais um método que você pode usar para lembrar facilmente as tabelas de fórmulas trigonométricas.

As etapas que você precisa fazer são as seguintes:

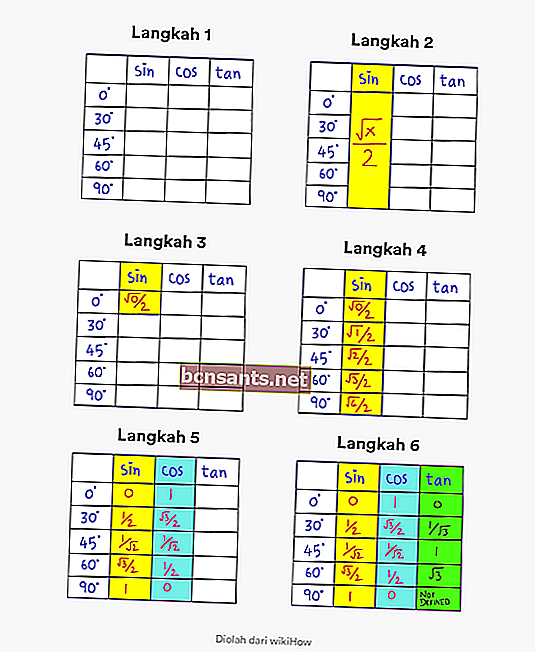
• Etapa 1 . Crie uma tabela que contenha ângulos de 0 - 90 graus e colunas com a descrição sin cos tan
• Etapa 2 . Observe que a fórmula geral para sin em um ângulo de 0 a 90 graus é √x / 2.
• Etapa 3 . Altere o valor x para 0 em √x / 2 na primeira coluna. Canto superior esquerdo.
• Etapa 4. Preencha a sequência alterando x para 0, 1, 2, 3, 4 na coluna sin. Assim você obteve o valor trigonométrico completo sen
• Etapa 5 . Para encontrar o valor de cos, tudo que você precisa fazer é inverter a ordem na coluna de pecado.
• Etapa 6 . Para encontrar o valor de tan, tudo o que você precisa fazer é dividir o valor do pecado pelo valor do cos.

Leia também: Histórias de ficção: exemplos, definição e elementos [FULL

Qual é mais fácil de entender para lembrar o valor trigonométrico de tan sin cos?

De qualquer forma, escolha aquele que for mais fácil de entender. Porque cada pessoa tem um estilo de aprendizagem diferente.

Tabelas para todos os ângulos

Se nas tabelas acima os valores mostrados forem apenas os valores trigonométricos de ângulos especiais, então esta tabela mostra todos os valores trigonométricos de todos os ângulos de 0 a 90 graus.

Canto	Radianos	Pecado	Cos	bronzeado
0 °	0	0	1	0
1 °	0,01746	0,01746	0,99985	0,01746
2 °	0,03492	0,03491	0,99939	0,03494
3 °	0,05238	0,05236	0,99863	0,05243
4 °	0,06984	0,06979	0,99756	0,06996
5 °	0,0873	0,08719	0,99619	0,08752
6 °	0,10476	0,10457	0,99452	0,10515
7 °	0,12222	0,12192	0,99254	0,12283
8 °	0,13968	0,13923	0,99026	0,1406
9 °	0,15714	0,1565	0,98768	0,15845
10 °	0,1746	0,17372	0,9848	0,1764
11 °	0,19206	0,19089	0,98161	0,19446
12 °	0,20952	0,20799	0,97813	0,21265
13 °	0,22698	0,22504	0,97435	0,23096
14 °	0,24444	0,24202	0,97027	0,24943
15 °	0,26191	0,25892	0,9659	0,26806
16 °	0,27937	0,27575	0,96123	0,28687
17 °	0,29683	0,29249	0,95627	0,30586
18 °	0,31429	0,30914	0,95102	0,32506
19 °	0,33175	0,32569	0,94548	0,34448
20 °	0,34921	0,34215	0,93965	0,36413
21 °	0,36667	0,35851	0,93353	0,38403
22 °	0,38413	0,37475	0,92713	0,40421
23 °	0,40159	0,39088	0,92044	0,42467
24 °	0,41905	0,40689	0,91348	0,44543
25 °	0,43651	0,42278	0,90623	0,46652
26 °	0,45397	0,43854	0,89871	0,48796
27 °	0,47143	0,45416	0,89092	0,50976
28 °	0,48889	0,46965	0,88286	0,53196
29 °	0,50635	0,48499	0,87452	0,55458
30 °	0,52381	0,50018	0,86592	0,57763
31 °	0,54127	0,51523	0,85706	0,60116
32 °	0,55873	0,53011	0,84793	0,62518
33 °	0,57619	0,54483	0,83854	0,64974
34 °	0,59365	0,55939	0,8289	0,67486
35 °	0,61111	0,57378	0,81901	0,70057
36 °	0,62857	0,58799	0,80887	0,72693
37 °	0,64603	0,60202	0,79848	0,75396
38 °	0,66349	0,61587	0,78785	0,78172
39 °	0,68095	0,62953	0,77697	0,81024
40 °	0,69841	0,643	0,76586	0,83958
41 °	0,71587	0,65628	0,75452	0,86979
42 °	0,73333	0,66935	0,74295	0,90094
43 °	0,75079	0,68222	0,73115	0,93308
44 °	0,76825	0,69488	0,71913	0,96629
45 °	0,78571	0,70733	0,70688	1,00063
46 °	0,80318	0,71956	0,69443	1.0362
47 °	0,82064	0,73158	0,68176	1.07308
48 °	0,8381	0,74337	0,666888	1,11137
49 °	0,85556	0,75494	0,6558	1,15117
50 °	0,87302	0,76627	0,64252	1,1926
51 °	0,89048	0,77737	0,62904	1.2358
52 °	0,90794	0,78824	0,61537	1.28091
53 °	0,9254	0,79886	0,60152	1,32807
54 °	0,94286	0,80924	0,58748	1,37748
55 °	0,96032	0,81937	0,57326	1.42932
56 °	0,97778	0,82926	0,55887	1,48382
57 °	0,99524	0,83889	0,5443	1,54122
58 °	1.0127	0,84826	0,52957	1,60179
59 °	1.03016	0,85738	0,51468	1.66584
60 °	1.04762	0,86624	0,49964	1,73374
61 °	1.06508	0,87483	0,48444	1,80587
62 °	1.08254	0,88315	0,46909	1,8827
63 °	1,1	0,89121	0,4536	1.96476
64 °	1,11746	0,89899	0,43797	2.05265
65 °	1.13492	0,9065	0,4222	2,14707
66 °	1,15238	0,91373	0,40631	2,24884
67 °	1,16984	0,92069	0,3903	2.35894
68 °	1,1873	0,92736	0,37416	2,4785
69 °	1.20476	0,93375	0,35792	2,60887
70 °	1.22222	0,93986	0,34156	2,75169
71 °	1.23968	0,94568	0,3251	2,90892
72 °	1.25714	0,95121	0,30854	3.08299
73 °	1.2746	0,95646	0,29188	3,27686
74 °	1,29206	0,96141	0,27514	3.49427
75 °	1,30952	0,96606	0,25831	3,73993
76 °	1.32698	0,97043	0,2414	4.01992
77 °	1.34444	0,97449	0,22442	4.34219
78 °	1,36191	0,97826	0,20738	4.71734
79 °	1,37937	0,98173	0,19026	5,15984
80 °	1,39683	0,98491	0,1731	5,68998
81 °	1,41429	0,98778	0,15587	6,33709
82 °	1,43175	0,99035	0,1386	7,14523
83 °	1.44921	0,99262	0,12129	8.18379
84 °	1,46667	0,99458	0,10394	9.56868
85 °	1,48413	0,99625	0,08656	11,5092
86 °	1,50159	0,99761	0,06915	14.4259
87 °	1.51905	0,99866	0,05173	19,3069
88 °	1,53651	0,99941	0,03428	29.153
89 °	1,55397	0,99986	0,01683	59,4189
90 °	1,57143	1	0	∞

Esperançosamente, esta explicação trigonométrica pode ser útil para você.

Este material será de grande utilidade para várias aplicações em matemática e física avançadas.

Você também pode aprender outros materiais escolares na Saintif, como números primos, conversões de unidades, fórmulas retangulares e assim por diante.

Referência

• Trigonometria - Wikipedia
• Ferramentas matemáticas - trigonometria