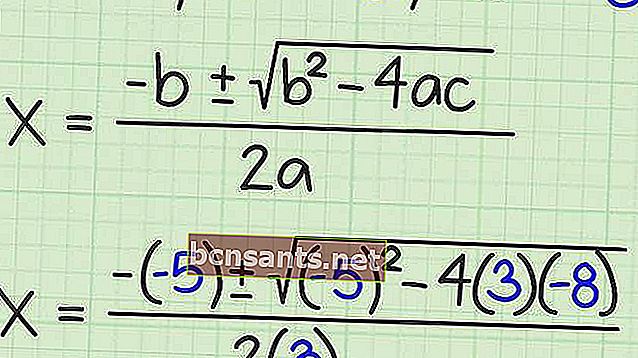
A fórmula ABC é uma excelente maneira de encontrar as raízes de várias formas de equações quadráticas, mesmo se o resultado não for um número inteiro.
A equação quadrática ax2 + bx + c = 0 pode ser resolvida usando vários métodos. Entre eles estão o método de fatoração, completando o quadrado ABC e fórmula.
Entre esses métodos, a fórmula abc é excelente porque pode ser usada para encontrar as raízes de várias formas de equações quadráticas, mesmo se o resultado não for um número inteiro.
A seguir está uma explicação adicional da fórmula, incluindo compreensão, perguntas e discussão.
Compreendendo a fórmula ABC
A fórmula abc é uma das fórmulas usadas para encontrar as raízes de uma equação quadrática. Aqui está uma forma geral desta fórmula.

As letras a, b e c na fórmula abc são chamadas de coeficientes. O coeficiente de x2 ao quadrado é a, o coeficiente de x é b e c é o coeficiente da constante, geralmente referido como um termo constante ou independente.
A equação quadrática é basicamente uma equação matemática que forma a geometria curva da parábola no quadrante xy.
O valor do coeficiente na fórmula abc tem vários significados, como segue:
- a determina a prábola côncava / convexa formada pela equação quadrática. Se o valor de a> 0, a parábola abrirá para cima. No entanto, se a <0, a parábola abrirá para baixo.
- b determina a posição x do pico parabólico ou o valor simétrico de espelho da curva. A posição exata do eixo de simetria é -b / 2a da equação quadrática.
- c determina o ponto de interseção da função de equação quadrática parabólica formada no eixo y ou quando o valor x = 0.
Exemplos de perguntas e discussão
Aqui estão alguns exemplos de problemas de equação quadrática e sua discussão com soluções usando fórmulas de equação quadrática.
1. Resolva as raízes da equação quadrática x2 + 7x + 10 = 0 usando a fórmula abc!
Responda:
Leia também: 7 funções de proteínas para o corpo [explicação completa]observe que a = 1, b = 7 e c = 10
então, as raízes da equação são:

Então, o produto das raízes da equação x2 + 7x + 10 = 0 é x = -2 ou x = -5
2. Usando a fórmula abc, encontre o conjunto de soluções para x2 + 2x = 0
Responda:
dado que a = 1, b = 1, c = 0
então as raízes da equação são as seguintes:

Assim, o produto das raízes da equação x2 + 2x = 0 é x1 = 0 e x2 = -2, então o conjunto de soluções é HP = {-2,0}
3. Encontre o conjunto de raízes x no problema x2 - 2x - 3 = 0 usando a fórmula abc
Responda:
dado que a = 1, b = 2, c = -3
então, os resultados das raízes da equação são os seguintes:

Assim, com x1 = -1 e x2 = -3, o conjunto de soluções é HP = {-1,3}
4. Determine o resultado da equação quadrática x 2 + 12x + 32 = 0 usando a fórmula abc !
Responda:
observe que a = 1, b = 12 e c = 32
então as raízes da equação são as seguintes:

Então, os resultados das raízes para a equação quadrática são -4 e -8
5. Encontre o conjunto do seguinte problema 3x2 - x - 2 = 0
Responda:
observe que a = 3, b = -1, c = -2
então as raízes da equação são as seguintes:

Assim, as raízes da equação quadrática 3x2 - x - 2 = 0 são x1 = 1 e x2 = -2 / 3, então o conjunto de soluções é HP = {1, -2 / 3}
6. Encontre as raízes da equação x 2 + 8x + 12 = 0 usando a fórmula abc!
Responda:
observe que a = 1, b = 8 e c = 12
então, as raízes da equação quadrática são as seguintes:

Assim, as raízes da equação quadrática x2 + 8x + 12 = 0 são x1 = -6 ou x2 = -2 de modo que o conjunto de soluções é HP = {-6, -2}
7. Resolva as raízes da equação x 2 - 6x - 7 = 0 com a fórmula abc .
Responda:
sabe-se que a = 1, b = - 6 e c = - 7
então as raízes da equação são as seguintes:
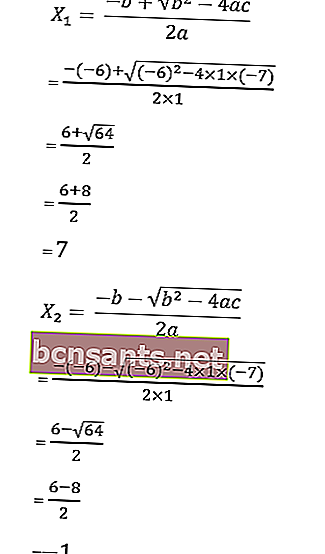
Portanto, as raízes são x 1 = 1 ou x 2 = 5/2, então o conjunto de soluções é HP = {1, 5/2}.
Leia também: Equações quadráticas (COMPLETO): Definição, Fórmulas, Problemas de Exemplo8. Encontre as raízes da equação 2x 2 - 7x + 5 = 0 com a fórmula abc
Responda:
sabemos que a = 2, b = - 7 e c = 5
então as raízes da equação são as seguintes:
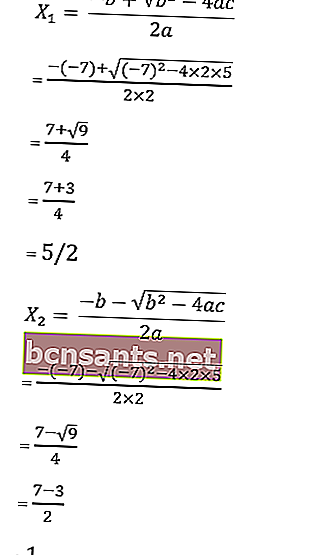
Portanto, as raízes são x1 = –4 ou x2 = 5/3 de modo que o conjunto de soluções é HP = {1, 5/3}.
9. Resolva a equação 3x 2 + 7x - 20 = 0 com a fórmula abc.
Responda:
sabe-se que a = 3, b = 7 e c = - 20
então as raízes da equação são:
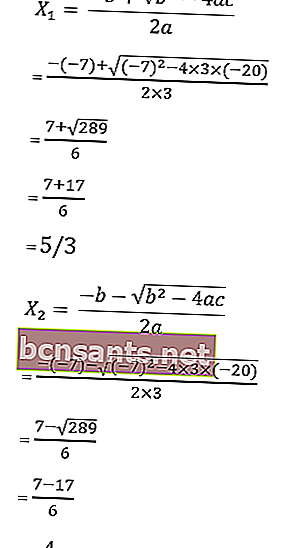
Portanto, as raízes são x1 = –4 ou x2 = 5/3, então o conjunto de soluções é HP = {-4, 5/3}.
10. Encontre as raízes da equação 2x 2 + 3x +5 = 0 com a fórmula abc.
Responda:
sabemos que a = 2, b = 3 e c = 5
então as raízes da equação são as seguintes:
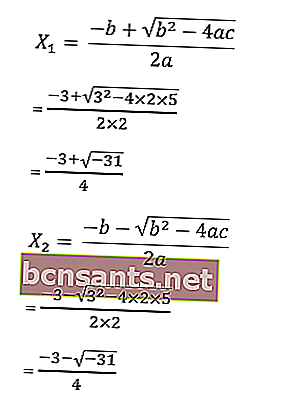
O resultado da raiz da equação 2x2 + 3x +5 = 0 tem o número da raiz imaginária √ - 31, então a equação não tem solução. O conjunto de soluções é escrito como o conjunto vazio HP = {∅}
Esta é uma explicação da definição da fórmula abc com exemplos de perguntas e sua discussão. Pode ser útil!
