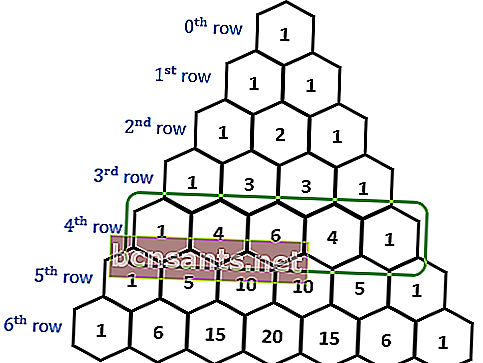
O triângulo de Pascal é um arranjo de triângulos criado pela adição de elementos adjacentes na linha anterior. Este arranjo de triângulos é feito adicionando elementos adjacentes na linha anterior.
Suponha que as variáveis a e b sejam somadas e depois elevadas à potência de 0 à potência de 3, o resultado é a seguinte descrição.
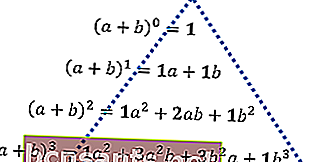
Em seguida, considere a disposição dos números em negrito de cima para baixo, até encontrar a forma de um triângulo. Este padrão numérico é doravante denominado triângulo de Pascal.
Compreendendo o Triângulo de Pascal
O triângulo de Pascal é a regra geométrica do coeficiente binomial em um triângulo.
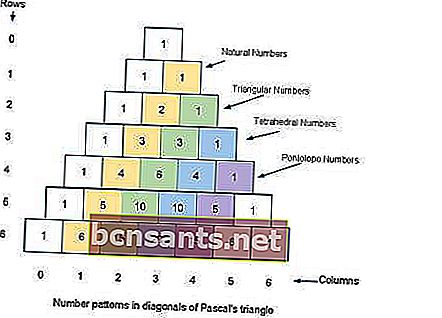
O triângulo tem o nome do matemático Blaise Pascal, embora outros matemáticos o tenham estudado séculos antes dele na Índia, Pérsia, China e Itália.
Conceito de Regras
O conceito de triângulo de Pascal é um sistema de cálculo para este triângulo, independentemente das variáveis a e b. Isso significa que basta atentar para o coeficiente binomial, da seguinte forma:
- Na linha zero, escreva apenas o número 1.
- Em cada linha abaixo, escreva o número 1 à esquerda e à direita.
- A soma dos dois números acima, escritos na linha abaixo.
- 1 à esquerda e à direita de acordo com (2), sempre circunda o resultado (3)
- Os cálculos podem continuar com o mesmo padrão.
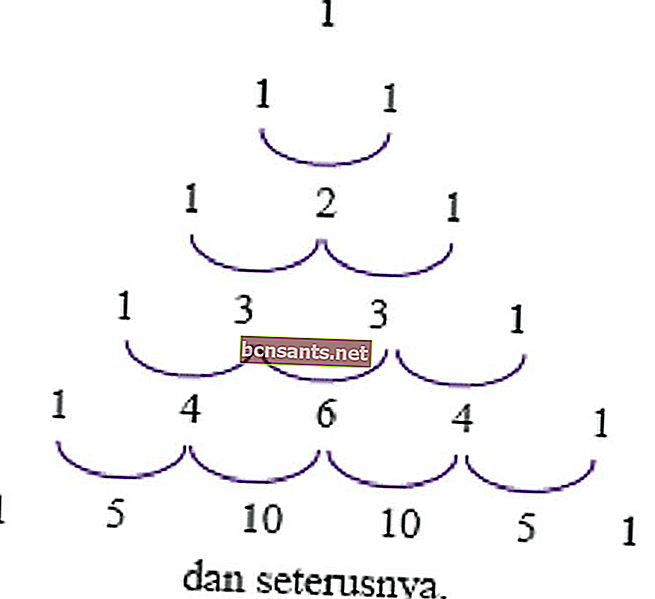

Um uso desse triângulo é determinar o coeficiente em potência (a + b) ou (ab) para torná-lo mais eficiente. Esse uso é descrito nos exemplos a seguir.
Exemplo de problemas
Dica: preste atenção ao triângulo de Pascal.
1. Qual é a tradução (a + b) 4?
Solução : Para (a + b) 4
- Primeiro, as variáveis a e b são organizadas, começando em a4b ou a4
- Então, a potência de a cai para 3, que é a3b1 (o total à potência de ab deve ser 4)
- Em seguida, a potência de a cai para 2, tornando-se a2b2
- Então a potência de a cai para 1, tornando-se ab3
- Então, a potência de a cai para 0, para b4
- Em seguida, escreva a equação com o coeficiente na frente do branco
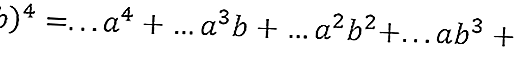
De acordo com a Figura 2 na 4ª ordem, os números 1,4,6,4,1 são obtidos, então a tradução (a + b) 4 é obtida

2. Qual é o coeficiente a3b3 em (a + b) 6?
Leia também: Material do campo magnético: fórmulas, exemplos de problemas e explicaçõesSolução :
Com base na questão número 1, a ordem das variáveis de (a + b) 6 é organizada, a saber
a6, a5b1, a4b2, a 3 b 3 .
Isso significa que na quarta ordem (figura 2, sequência 6) no padrão 1, 6, 15, 20 é 20 . Assim, 20 a3b3 pode ser escrito.
3. Determine a tradução de (3a + 2b) 3
Assentamento
A fórmula geral para o triângulo de Pascal como a soma das variáveis aeb à potência de 3 é apresentada a seguir

Alterando as variáveis para 3a e 2b, obtemos

