
Integral indefinido ou também conhecido como anti-derivado é uma forma de operação de integração que produz uma nova função .
Integral desempenha um papel muito importante na matemática. A teoria pode determinar a área sob a curva de uma função.
Integral é útil para o limite de soma que é contínuo em uma função contínua. Integral é anti-derivado. Então, se f é uma função contínua, o resultado integral da função f é denotado por F.
Os tipos integrados são baseados em certos limites funcionais que são incertos. A seguir está uma discussão para os tipos de integrais com limites indefinidos.
Integral indefinida
Uma integral indefinida ou também conhecida como anti-derivada ou anti-diverencial é uma forma de operação de integração que produz uma nova função.
Considere a seguinte equação.

com C uma constante. A fórmula integral indefinida é a seguinte
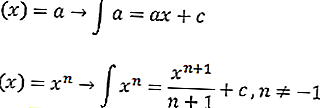
ou igual a

com
- a (x) ^ n = função de equação
- a = constante
- x = variável
- n = Potência da função de equação
- C = constante
O resultado dessa integral indefinida é uma função que é uma função nova que não tem um valor certo ou definido porque ainda existem variáveis na nova função.
Para que você possa entender melhor o conceito de integral indeterminada, considere o problema de exemplo abaixo.

Com base neste exemplo, uma operação integral pode ser formulada, a saber
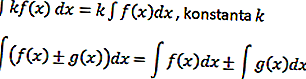
Integral trigonométrico
A integral de uma função não é necessariamente uma constante, linear ou polinomial. Nesta solução intergal, muitas vezes envolve elementos trigonométricos.
Na função trigonômica, as definições de integrais que são organizadas na tabela a seguir também se aplicam.
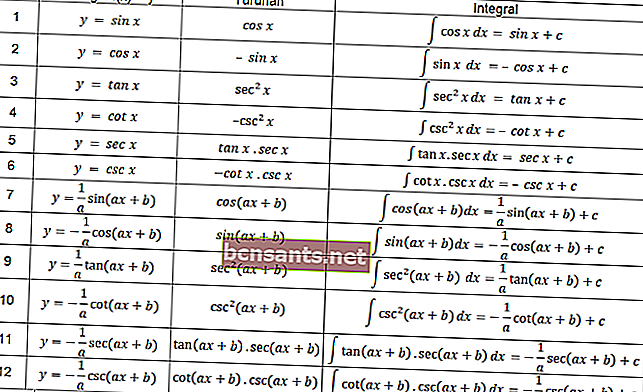
Você pode usar as equações da tabela acima para resolver o problema integral que envolve trigonometria.
Para entender melhor os integrais trigonométricos, você pode entender os exemplos a seguir
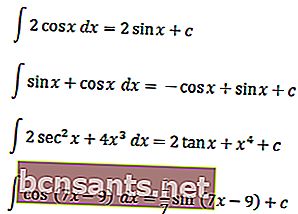
Essa foi a explicação das integrais indeterminadas em funções trigonométricas ordinárias e especiais. Esperançosamente, pode ser bem estudado.
Leia também: As normas de decência: Definição, Objetivos, Sanções e Exemplos [COMPLETO]Para entender melhor o conceito desta integral, você pode praticar fazendo perguntas práticas. Se houver algo que você queira perguntar, escreva na coluna de comentários.
