
O valor absoluto em cálculo é muito útil para resolver vários problemas matemáticos, tanto em equações quanto em desigualdades. A seguir está uma explicação completa dos valores absolutos e exemplos de perguntas.
Definição de valor absoluto
Todos os números têm seus respectivos valores absolutos. Todos os números absolutos são positivos, portanto, os valores de número absoluto de números com o mesmo número, mas com notações positivas (+) e negativas (-) diferentes, terão o mesmo resultado de número absoluto.
Se x for membro de um número real, o valor absoluto será escrito como | x | e é definido da seguinte forma:

"Valor absoluto é um número com o mesmo valor de comprimento ou distância da origem ou ponto zero nas coordenadas."
Pode ser interpretado que o valor absoluto de 5 é o comprimento ou distância do ponto 0 ao ponto 5 ou (-5).
Os valores absolutos de (-9) e 9 são 9. Os valores absolutos de 0 são 0 e assim por diante. Nilaa
Eu vou entender isso perfeitamente olhando para a seguinte imagem:

Na foto acima, pode-se entender que o valor de | 5 | é a distância do ponto 5 ao número 0, a saber 5, e | -5 | a distância do ponto (-5) ao número 0 é 5.
Se | x | representa a distância do ponto x a 0, então | xa | é a distância do ponto x ao ponto a. Por exemplo, ao expressar a distância do ponto 5 ao ponto 2, pode ser escrito como | 5-2 | = 3

Em geral, pode-se afirmar que a distância x a a pode ser escrita com a notação | xa | ou | machado |
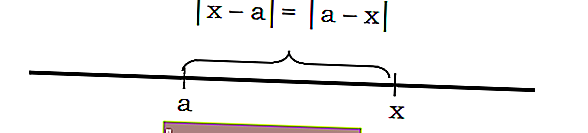
Por exemplo, a distância de um número ao ponto 3 vale 7 da seguinte forma:
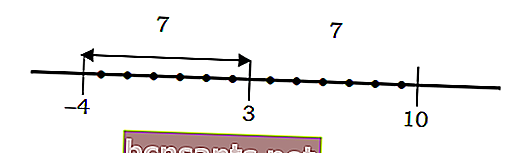
Se descrito na equação algébrica | x-3 | = 7, pode ser resolvido da seguinte forma:
Leia também: Medindo Terremotos com Logaritmos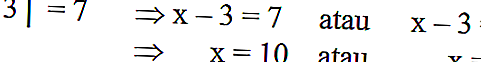
Lembre-se de que | x-3 | é a distância do número x ao ponto 3, onde | x-3 | = 7 é a distância do número x ao ponto 3 para 7 unidades.
Propriedades de valor absoluto
Em operações de equação de número absoluto, existem propriedades de número absoluto que podem ajudar a resolver equações de número absoluto.
A seguir estão as propriedades dos números absolutos em geral nas equações de valor absoluto:

As propriedades do valor absoluto da desigualdade:
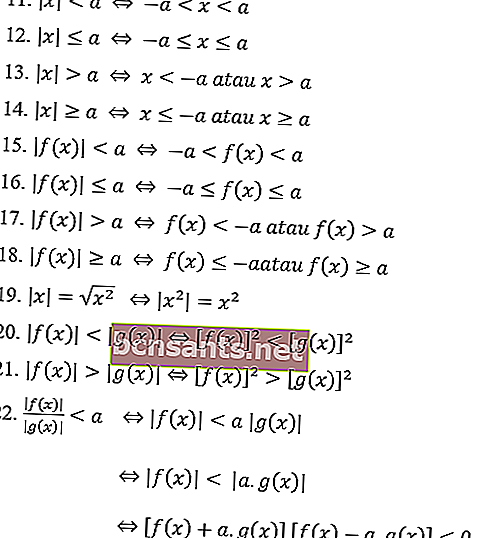
Exemplos de problemas de equação de valor absoluto
Exemplo de problema 1
Qual é o valor absoluto da equação | 10-3 |?
Responda:
| 10-3 | = | 7 | = 7
Exemplo de problema 2
Qual é o resultado de x para a equação do valor absoluto | x-6 | = 10?
Responda:
Para resolver esta equação, existem dois resultados possíveis para números absolutos
| x-6 | = 10
Primeira solução:
x-6 = 10
x = 16
segunda solução:
x - 6 = -10
x = -4
Portanto, a resposta a esta equação é 16 ou (-4)
Exemplo de problema 3
Resolva e calcule o valor x na seguinte equação
–3 | x - 7 | + 2 = –13
Responda:
–3 | x - 7 | + 2 = –13
–3 | x - 7 | = –13 - 2
–3 | x - 7 | = –15
| x - 7 | = –15 / –3
| x - 7 | = 5
Feito até a solução acima, então o valor x tem dois valores
x - 7 = 5
x = 12
ou
x - 7 = - 5
x = 2
então o valor x final é 12 ou 2
Exemplo de problema 4
Resolva a seguinte equação e qual é o valor de x
| 7 - 2x | - 11 = 14
Responda:
| 7 - 2x | - 11 = 14
| 7 - 2x | = 14 + 11
| 7 - 2x | = 25
Depois de completar a equação acima, os números para o valor absoluto de x são os seguintes
7 - 2x = 25
2x = - 18
x = - 9
ou
7 - 2x = - 25
2x = 32
x = 16
Portanto, o valor final de x é (- 9) ou 16
Exemplo de problema 5
Encontre a solução para a seguinte equação de valor absoluto:
| 4x - 2 | = | x + 7 |
Responda:
Para resolver a equação acima, use duas soluções possíveis, a saber:
Leia também: Erros na leitura dos resultados estatísticos da pesquisa de elegibilidade dos candidatos presidenciais4x - 2 = x + 7
x = 3
ou
4x - 2 = - (x + 7)
x = - 1
Portanto, a solução para a equação | 4x - 2 | = | x + 7 | é x = 3 ou x = - 1
Exemplo de problema 6
Determine a solução para a seguinte equação de valor absoluto:
| 3x + 2 | ² + | 3x + 2 | - 2 = 0
Qual é o valor de x?
Responda:
Simplificação: | 3x + 2 | = p
então
| 3x + 2 | ² + | 3x + 2 | -2 = 0
p² + p - 2 = 0
(p + 2) (p - 1) = 0
p + 2 = 0
p = - 2 (o valor absoluto não é negativo)
ou
p - 1 = 0
p = 1
| 3x + 2 | = 1
Até a solução acima, existem 2 respostas possíveis para x, a saber:
3x + 2 = 1
3x = 1 - 2
3x = - 1
x = - 1/3
ou
- (3x + 2) = 1
3x + 2 = -1
3x = - 1 - 2
3x = - 3
x = - 1
Portanto, a solução para a equação é x = - 1/3 ou x = - 1
Referência: valor absoluto - matemática é divertido
