
Discutirei as fórmulas para volume de blocos e área de superfície dos blocos neste artigo, considerando que esse material é frequentemente solicitado em problemas de matemática do ensino fundamental e médio.
A seguir está a fórmula para o volume e a área de um bloco.
| Volume do bloco | V = pxlxt |
| Área de superfície do bloco | L = 2 x (pl + pt + lt) |
| Feixe diagonal | d = √ ( p2 + l2 + t2) |
Continue lendo a explicação abaixo para obter um entendimento mais completo junto com exemplos de perguntas.

Definição de viga
Um bloco é uma forma tridimensional formada por pares de três pares de retângulos.
Você pode encontrar blocos de construção na vida cotidiana. Um exemplo é
- O smartphone que você está usando
- papelão embrulho para presente
- o livro que você leu
- e muitos outros.
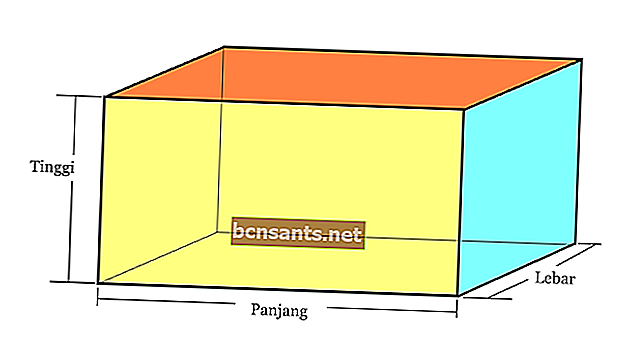
O bloco tem um total de 6 lados, 12 arestas e 8 pontos de canto. Os lados do bloco, nomeadamente o comprimento, largura e altura, têm comprimentos diferentes. Se os lados forem iguais, a forma é chamada de cubo.
Em geral, em matéria de matemática, há três quantidades que são solicitadas a serem procuradas nos blocos, a saber:
- Volume do bloco
- Área de feixe
- O comprimento da diagonal dos blocos.
Então, como você calcula esses valores? Imediatamente, discutimos.
Fórmula de volume do bloco
Volume = comprimento x largura x altura
V = pxlxt
A fórmula para calcular o volume de um bloco é muito simples. Você só precisa multiplicar os três lados do bloco, ou seja, comprimento, largura e altura.
Você pode ver a imagem a seguir para mais detalhes.
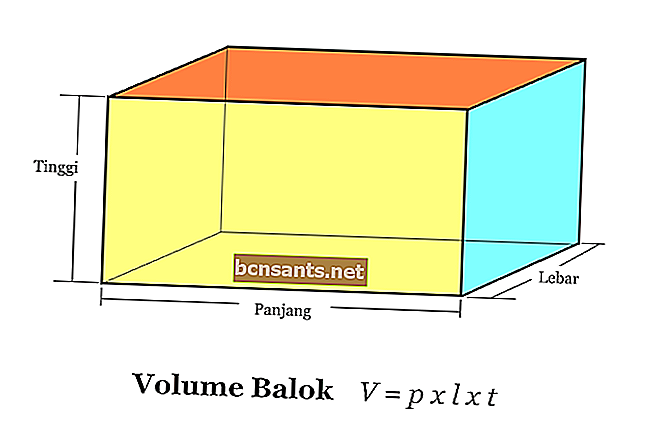
Uma coisa importante que você precisa prestar atenção ao calcular o volume deste bloco é que você deve expressar o comprimento de todos os lados em uma unidade igual.
Suponha que você declarou o comprimento em cm, então você também deve expressar a largura e a altura em cm, para que o resultado seja correto.
Leia também: O Processo da Chuva (+ Imagem Completa e Explicação)A unidade para o volume de balol é a unidade de comprimento cúbico ou cúbico. Por exemplo, m3 (metro cúbico), cm3 (centímetro cúbico) e assim por diante.
Você também pode converter este valor de volume em outras unidades usando a técnica de conversão de unidades.
Fórmula da Área do Bloco
L = 2 x (pl + pt + lt)
Ao contrário da fórmula para o volume de um bloco, que se faz multiplicando os três lados, a fórmula para a área do bloco é um pouco mais longa.
Você precisa calcular a área de cada retângulo e multiplicar por dois.

Você pode ver a fórmula de resumo acima.
O que você precisa prestar atenção, ao calcular essa área, suas unidades devem ser as mesmas. Para que os resultados da sua contagem estejam corretos.
A fórmula para a diagonal dos blocos
O comprimento da diagonal do bloco é o comprimento que conecta um vértice a outro vértice oposto a ele.
Para calcular o comprimento de onda, precisamos calcular o comprimento do lado do triângulo usando a fórmula pitagórica.
A forma de calcular o comprimento da diagonal dos blocos é a seguinte:

A seguir, vamos praticar resolver os problemas.
Exemplo 1 problema de matemática de bloco
Um bloco tem 200 cm de comprimento, 10 cm de largura e 20 cm de altura. Calcule a área e o volume do bloco.
RESPONDA
Volume do bloco:
V = pxlxt
V = (200) x (10) x (20)
V = 40.000 cm3
Área de feixe
L = 2 x (pl + pt + lt)
L = 2 x ((200) (10) + (200) (20) + (10) (20))
L = 2 x (6200)
L = 12400 cm2
Exemplo 2 Problema de fórmula de volume de bloco
Você sabe que um bloco tem um comprimento de 10 m, uma largura de 2 m e uma altura de 100 cm. Calcule o volume do bloco.
RESPONDA
O método para calcular o volume do bloco é na verdade o mesmo do problema do exemplo anterior.
No entanto, deve-se notar que as unidades de medição dos lados da viga não são as mesmas.
Portanto, temos que igualar primeiro.
Comprimento, p = 10 m
Largura, l = 2 m
Altura, h = 100 cm = 1 m
Em seguida, calcule a fórmula do bloco:
V = pxlxt
V = 10 x 2 x 1
V = 20 m3
Exemplo 3: Problema de Matemática Diagonal de Bloco
Calcule o comprimento da diagonal dos blocos no problema de exemplo número 1 e número 2 acima.
Problema número 1:
p = 200 m, l = 10 m, t = 20 m.
O comprimento da diagonal dos blocos =
d = √ ( p2 + l2 + t2)
d = 201,25 m.
Leia também: Pluralidade: definição, discussão e exemplosProblema número 2:
p = 10 m, l = 2 m, t = 1 m
O comprimento da diagonal dos blocos
d = √ ( p2 + l2 + t2)
d = √ 105
d = 10,25 m
Exemplo 4 Fórmula do bloco da história do problema
Mamãe comprou um bloco de gelo com volume de 10 m3. Se você sabe que o bloco de gelo tem 2,5 m de comprimento e 2 m de largura, qual é a altura do bloco de gelo?
RESPONDA
Você pode responder a este problema usando a fórmula básica para o volume de blocos.
V = pxlxt
10 = (2,5) x (2) xt
10 = 5 xt
t = 10/5 = 2 m
O bloco de gelo tem 2 m de altura
Exemplo 5 Fórmulas de bloco de histórias de problema
O Ridho possui uma piscina em forma de bloco. tem uma piscina que originalmente continha até 600 litros de água. Então Ridho drenou a piscina de forma que apenas 1/3 da água permaneceu de antes. Qual é a profundidade da água que resta na piscina se se sabe que a área da piscina é de 4 m2?
RESPONDA:
O volume inicial de água da piscina = 600 L.
O volume restante de água final = 1/3 x 600 = 200 L. Este valor é convertido em m3 para 0,2 m3
Sabe-se que a área do leito da piscina = 2 m2
A altura da água restante da piscina pode ser calculada usando a fórmula básica para o volume dos blocos.
V = pxlxt
V = (pxl) xt
V = (área da base) xt
0,2 = 2 xt
t = 0,1 m
h = 10 cm
Assim, o nível de água da piscina após a drenagem é de 10 cm.
Exemplo 6 Fórmulas de bloco de histórias de problema
Pak Budi compra toras da loja, cujos preços são calculados em unidades de volume. 1 m3 de madeira está avaliado em IDR 10.000. Se o Sr. Budi comprar um bloco de madeira medindo 8 m de comprimento, 1 m de largura e 1 m de altura, qual é o preço da madeira comprada?
RESPONDA
O volume de toras que o Sr. Budi comprou foi
V = pxlxt
V = (8) x (1) x (1)
V = 8 m3
Uma vez que cada 1 m3 de madeira custa Rp. 10.000, o preço das toras que o Sr. Budi está comprando
Preço = 8 x 10.000 = IDR 80.000
Como o dicionário entendeu o tema volume dos blocos e área dos blocos? Você já deve entender, pois há explicações e exemplos das questões acima.
Se ainda tiver dificuldades, você pode comentar abaixo.
Referência:
- Cubóide - Wolfram Alpha
- Volume do cuboide - matemática é divertida
