Coleção de fórmulas matemáticas para SD Classe 6

A seguinte coleção de fórmulas matemáticas para o SD da 6ª série consiste em:

Uma coleção de fórmulas de volume para construir espaço, fórmula para escala
Calculando a área plana
Operações Inteiras
Fórmulas de operação de contagem de números mistos
A Fórmula para FPB e KPK é Dois Números
Processando e apresentando dados
Sistema de Coordenadas, Fórmulas de Volume e Tempo
Adição e subtração de frações e determinação da raiz quadrada dos números cúbicos.

Fórmulas matemáticas da classe 6 Calculam o volume da construção de uma sala

Espaço para construir nomes	Fórmulas de Volume
Tubo	V = phi r² xt
Triângulo vertical Prima	V = Área da base x Altura

Classe 6 Escala de cálculo da coleção de fórmulas matemáticas

Fórmulas de escala	= Distância na imagem (Mapa) / Distância real
Fórmulas de distância na Fig	= Distância real x escala
Fórmulas de distância real	= Distância na imagem (mapa) / escala

Coleção de fórmulas para calcular a área de um plano

Figura bidimensional	Fórmula de área
Construir um quadrado plano	L = lado x lado = s²
Construa um Triângulo Plano	L = ½ base x altura
Construir um círculo plano	L = phi x r²
Trapezoidal Build	L = ½ t × (a + b)
Build Flat Kite - Kite	L = ½ xd ₁ xd ₂
Construir paralelogramo plano	L = Base x Altura
Retire o losango plano	L = ½ xd ₁ xd ₂
Construir retângulo plano	L = Comprimento x Largura

Coleção de fórmulas de operação de número inteiro SD Classe 6

Propriedades comutativas de adição, fórmulas gerais: a + b = b + a

Por exemplo: 2 + 4 = 4 + 2 = 6 ou 5 + 10 = 10 + 5 = 15

Natureza comutativa da multiplicação, Fórmulas Gerais: axb = bxa

Por exemplo: 3 x 5 = 5 x 3 = 15 ou 10 x 2 = 2 x 10 = 20

Propriedades distributivas de multiplicação para adição

Fórmula geral: ax (b + c) = (axb) + (axc)

Exemplo:

2 x (5 + 10)	= 2 x 5 + 2 x 10
	= 10 + 20
	= 30

Natureza distributiva da multiplicação para subtração

Fórmula geral: ax (b - c) = (axb) - (axc)

Exemplo:

2 x (10 - 5)	= 2 x 10 - 2 x 5
	= 20 + 10
	= 10

Coleção de fórmulas de operações de cálculo de números mistos

A Operação de Cálculo de Números Mistos possui 2 Condições, a saber, entre outras:

Leia também: Características dos planetas no sistema solar (COMPLETO) com imagens e explicações

Primeiro, se houver colchetes (), faça o que está dentro dos colchetes primeiro.

Segundo, se não houver colchetes (), faça Multiplicação e Divisão primeiro e, em seguida, Adição e Subtração.

Exemplo:

= 7.000 - 40 x 100: 4 + 200		= 1000: 10 x 2 - (200 + 50)
= 7.000 - 1000 + 200		= 1000: 10 x 2 - 150
= 6200	Ou	= 100 x 2 - 150
		= 200 - 150
		= 50

A Fórmula para FPB e KPK é Dois Números

Como Determinar o FPB (Maior Fator Comum) Dois Números, entre outros, Encontre o Fator em cada um desses números, determine o Fator Comum dos dois números e Multiplique o Fator Comum (mesmo fator) que tem a menor potência.

Exemplo:

27	= 3³
18	= 2 x 3²

O fator comum para o FPB de dois números é 3, e a potência mais baixa é 3² = 9

Como determinar o MMC (mínimo múltiplo comum) para dois números, entre outros, encontre o fator primo de cada um desses números, multiplique todos os fatores e fatores que são iguais, o posto mais alto é escolhido.

Por exemplo: valores KPK 12 e 15

12	= 2² x 3
15	= 3 x 5

LCM valor dois números acima: 2² x 3 x 5 = 50

Processando e apresentando dados

Modo é o valor que mais aparece.

O valor mínimo é o menor e o menor valor de todos os dados.

O valor máximo é o valor mais alto de todos os dados nele.

A média é para que a média seja obtida somando todas as amostras divididas pelo número de amostras.

Encontrando o Sistema de Coordenadas
O eixo x também é chamado de Absis (x) e o eixo y é também chamado de ordenada (y).
Um plano de coordenadas cartesianas será formado por 2 eixos, a saber, o eixo vertical (eixo y) e o eixo horizontal (eixo x).
Do ponto zero, o eixo vertical estará para cima e o eixo horizontal estará à direita, o que tem um valor positivo.
Do ponto zero, o eixo vertical irá para baixo e o eixo horizontal irá para a esquerda, que tem um valor negativo.
Encontrar as coordenadas de um objeto pode ser encontrado encontrando a localização no eixo x à direita ou à esquerda com a posição no eixo y para cima ou para baixo.

Leia também: Questões de Matemática da Classe 6 (+ Discussão) SD UASBN - Completo

Relacionamento de Unidade de Volume

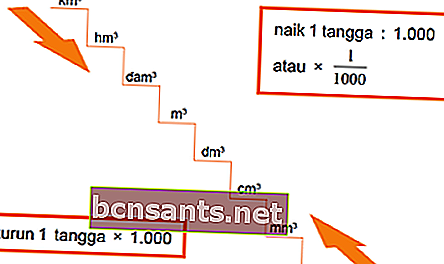
Exemplo:

1 km3 = 1.000 hm3 (descer 1 escada)

1 m3 = 1.000.000 cm3 (descer 2 escadas)

1 m3 = 1 / 1.000 dam3 (subir 1 escada)

1 m3 = 1 / 1.000.000 hm3 (subir 2 escadas)

Volume em litros

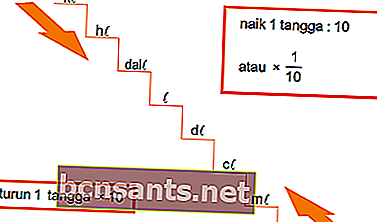
Unidade de Tempo

Um minuto	= 60 segundos
Uma hora	= 60 minutos
Um dia	= 24 horas
Uma semana	= 7 dias
Um mês	= 30 dias / 31 dias
Um mês	= 4 semanas
Um ano	= 52 semanas
Um ano	= 12 meses
Um Windu	= 8 anos
Uma década	= 10 anos
Uma década	= 10 anos
Um século	= 100 anos
Um milênio	= 1000 anos

Conversão de segundos

1 minuto = 60 segundos
1 hora = 3 600
1 dia = 86 400
1 mês = 2 592 000 segundos
1 ano = 31 104 000 segundos

Adição e subtração de frações

Para ser capaz de somar e subtrair frações, primeiro equalize os denominadores.

Exemplo:

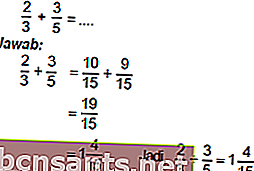
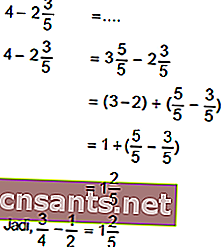
Multiplicando e dividindo frações

Multiplicar frações é bastante fácil. O numerador vezes o numerador. O denominador vezes o denominador. Se puder ser simplificado, simplifique:

A divisão fracionária é o mesmo que multiplicar pelo divisor da fração.

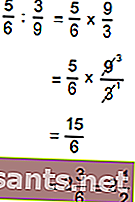
Encontre a raiz do cubo de um número cúbico

13 é lido como uma potência de três = 1 × 1 × 1 = 1

23 é lido como dois elevado a três = 2 × 2 × 2 = 8

33 é lido como três cubos = 3 × 3 × 3 = 27

43 é lido como quatro elevado a três = 4 × 4 × 4 = 64

53 é lido como cinco elevado a três = 5 × 5 × 5 = 125

1, 8, 27, 64, 125 e assim por diante são números cúbicos ou potências de 3

Adição e subtração

23 + 33 = (2 × 2 × 2) + (3 × 3 × 3)

= 8 + 27

= 35

63 - 43 = (6 × 6 × 6) - (4 × 4 × 4)

= 216 - 64

= 152

Multiplicação e divisão

23 × 43 = (2 × 2 × 2) × (4 × 4 × 4)

= 8 × 64

= 512

63: 23 = (6 × 6 × 6): (2 × 2 × 2)

= 216: 8

= 27

Essa é uma coleção de fórmulas de matemática do 6º ano do ensino fundamental que costumam aparecer nas questões do Exame Final Nacional (UAN) e do Exame Nacional (ONU). Pode ser útil.