
A fórmula do perímetro é K = 2 × π × r, onde K = a circunferência do círculo, π = a constante pi (3.14) er = o raio do círculo. A seguir está uma explicação mais completa acompanhada por um exemplo de problema.
A invenção da roda é uma das descobertas fundamentais sobre a importância das formas circulares na vida cotidiana.
Não apenas rodas, ainda existem muitas aplicações circulares se olharmos ao redor, como pneus de automóveis, moedas, relógios de parede, pirulitos, fitas de DVD, tampas de garrafa, salmos e outros.

Ok, tão importante não é esta forma de círculo? Obviamente, muito importante. Então, vamos aprender mais sobre círculo e fórmulas de círculo.
Construa um Círculo
Um círculo é uma forma bidimensional que consiste em um conjunto de pontos formando curvas / curvas que têm o mesmo comprimento no centro do círculo. Aqui, o ponto P é o centro do círculo.
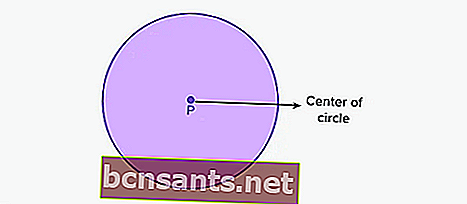
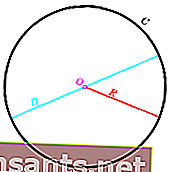
O mesmo comprimento ou distância em todos os pontos do centro do círculo é chamado de raio do círculo . Enquanto isso, a distância mais longa conectando os pontos externos de um círculo é chamada de diâmetro do círculo.
Além do raio e do diâmetro, um círculo tem outros elementos como um círculo, um arco circular, um esqueleto e uma corda.
A forma de um círculo também possui uma área e uma circunferência. Na próxima discussão, vamos nos concentrar apenas em discutir a fórmula para a circunferência de um círculo completo, juntamente com um exemplo de problema.
A fórmula para a circunferência de um círculo
A circunferência de um círculo é a distância de um ponto no círculo em uma volta para retornar ao ponto original. ou também pode ser interpretado como uma medida do comprimento do próprio círculo.
Suponha que temos um experimento, existem três objetos diferentes que são de forma circular. Em seguida, medimos a circunferência e o diâmetro do círculo do objeto. Conforme mostrado na tabela abaixo:
Por exemplo, se tivermos uma pulseira de metal. Em seguida, a pulseira é cortada para formar uma barra de metal reta, o comprimento da barra de metal é a circunferência da pulseira ou a circunferência do círculo.
| Coisa | Circunferência (K) | Diâmetro (d) | C / d = π |
| Lata de refrigerante | 24 cm | 7,7 cm | 3,11 |
| Latas de leite | 21,5 cm | 7,0 cm | 3,07 |
| Tupperware | 35,5 cm | 11 cm | 3,22 |
Depois disso, calculamos a razão entre a circunferência e o diâmetro e a média das três razões K / d do objeto é (3,11+ 3,07 +3,22) / 3 = 3,13.
Sim, a relação K / d está sempre próxima de 3,14 ou 22/7. Isso significa que a razão entre a circunferência de um círculo e o diâmetro é constante ou freqüentemente denotada por π (leia-se: phi).
Portanto, o valor de π = C / d = 3,14 ou 22/7
Se ambos os lados são multiplicados por d, obtemos,
C = π d
Em formação:
K = circunferência do círculo
d = diâmetro do círculo
π = 3,14 ou 22/7
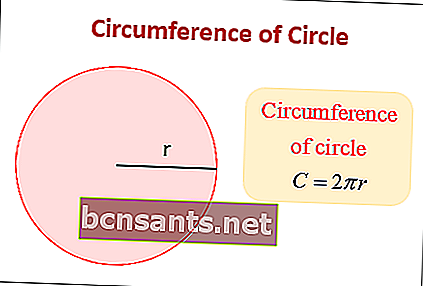
Uma vez que o diâmetro é igual a 2 x o raio do círculo d = 2r, a circunferência do círculo torna-se,
C = πd = π.2r
C = 2 π r
Em formação:
K = circunferência do círculo
r = o raio do círculo
π = 3,14 ou 22/7
Exemplo de problema com a fórmula da circunferência
1. A circunferência de um círculo é 396 cm. Calcule o raio do círculo!
Conhecido:
- K = 396 cm
Perguntou:
- r o raio do círculo?
Responda:
C = 2 π r
396 = 2 π r
396,7 = 2,22/7. r
r = 2772/44
r = 63 cm
Então, o raio do círculo é de 63 cm.
2. Encontre a circunferência de um círculo com raio de 14 cm com π = 22/7
Conhecido:
- r = 14 cm
- π = 22/7
Perguntou:
- Qual é a circunferência do círculo?
Responda:
C = 2 π r
K = 2 x 22/7 x 14
K = 2 x 22 x 2
K = 88 cm
Então, a circunferência do círculo é 88 cm
3. Encontre a circunferência de um círculo com um diâmetro de 10 cm com π = 3,14
Conhecido:
- d = 10 cm
- π = 3,14
Perguntou:
Qual é a circunferência do círculo?
Responda:
C = π d
K = 3,14 x 10
K = 31,4 cm
Portanto, a circunferência do círculo é 31,4 cm
4. Calcule a circunferência da área sombreada abaixo!
Conhecido:
- r = 14 cm
Perguntou:
Em torno da área sombreada?
Responda:
A imagem acima da circunferência consiste na circunferência de um quadrado mais metade do círculo e subtraída por um semicírculo, com o mesmo diâmetro e lado do quadrado, então a fórmula para a circunferência torna-se
Leia também: Os condutores são - Descrições, Desenhos e ExemplosCircunferência = 14 + 14 + ½ K + ½ K
= 14 + 14 + ½ π d + ½ π d
= 14 + 14 + ½. 22/7. 14 + ½. 22/7. 14
= 28 + 22+ 22
Circunferência = 72 cm
Portanto, a circunferência da área sombreada é igual a 72 cm.
5. Budi tem uma motocicleta que tem rodas com diâmetro de 84 cm e gira 1000 vezes, calcula a distância que o carro percorreu?
Conhecido:
- d = 84 cm
- n = 1000 vezes
Perguntou:
Quão longe a moto cobre?
Responda:
A distância percorrida pelo motor por 1000 vezes a circunferência do círculo = n / 2 = 1000/2 = 500
Então a distância percorrida pelo motor = 500x π d = 500,3,14. 84 = 131.880 cm = 1,31 km
6. Qual é a circunferência do círculo se o diâmetro é 40 cm?
Responda:
- Perímetro = π xd
- = 3,14 x 40
- = 125,66
Portanto, a circunferência do círculo é 125,66 cm.
7. Calcular a circunferência do círculo com diâmetro de 20 cm?
Solução:
Conhecido:
- d = 20 cm
- π = 3,14
Perguntado: Em torno do círculo?
Responda:
- Circunferência = π × d
- Circunferência = 3,14 × 20
- Circunferência = 62,8 cm
Portanto, a circunferência do círculo é 62,8 cm.
Esta é uma explicação completa das fórmulas completas para a circunferência de um círculo junto com um exemplo de problema. Pode ser útil!
Referência:
- Circunferências do Círculo - Khan Academy
- Como calcular circunferências de círculo - Wikihow
