
A fórmula do desvio padrão ou o que é conhecido como desvio padrão é uma técnica estatística usada para explicar a homogeneidade de um grupo.
O desvio padrão também pode ser usado para explicar como os dados são distribuídos em uma amostra, bem como a relação entre os pontos individuais e a média ou valor médio da amostra.
Antes de discutirmos mais, há algumas coisas que precisamos saber primeiro, a saber onde:
O desvio padrão do conjunto de dados pode ser zero ou maior ou menor que zero.
Esses valores variáveis têm significados, a saber:
- Se o desvio padrão for zero, todos os valores de amostra no conjunto de dados são iguais.
- Enquanto isso, o valor do desvio padrão maior ou menor que zero indica que o ponto de dados do indivíduo está longe do valor médio.

Passos para encontrar o desvio padrão
Para determinar e encontrar o valor do desvio padrão, precisamos seguir as etapas abaixo.
- O primeiro passo
Calcule a média ou valor médio em cada ponto de dados.
Você faz isso somando cada valor no conjunto de dados e, em seguida, o número é dividido pelo número total de pontos dos dados.
- O próximo passo
Calcule a variação dos dados calculando o desvio ou diferença para cada ponto de dados do valor médio.
O valor do desvio em cada ponto de dados é então elevado ao quadrado e removido pelo quadrado do valor médio.
Depois de obter o valor da variância, podemos calcular o desvio padrão fazendo o enraizamento do valor da variância.
Leia também: Narração: Definição, Propósito, Características, Tipos e ExemplosFórmulas de Desvio Padrão
1. Desvio Padrão da População
Uma população é simbolizada por σ (sigma) e pode ser definida pela fórmula:

2. Desvio Padrão da Amostra
A fórmula é:
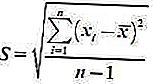
3. A fórmula para o desvio padrão de muitos grupos de dados
Para descobrir a distribuição dos dados de uma amostra, podemos reduzir cada valor dos dados pelo valor médio, então todos os resultados são somados.
No entanto, se você usar o método acima, o resultado sempre será zero, portanto, esse método não pode ser usado.

Para que o resultado não seja zero (0), devemos primeiro elevar ao quadrado a redução no valor dos dados e o valor médio, depois somar todos os resultados.
Usando este método, o resultado da soma dos quadrados terá um valor positivo.

O valor da variância será obtido dividindo a soma dos quadrados pelo número de tamanhos de dados (n).
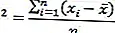
No entanto, se usarmos esse valor da variante para encontrar a variância da população, o valor da variância será maior do que a variante da amostra.
Para superar isso, o tamanho dos dados (n) como um divisor deve ser substituído por graus de liberdade (n-1) para que o valor da variância da amostra se aproxime da variante da população.
Assim, a fórmula da variante de amostra pode ser escrita como:

O valor da variante que foi obtido é o valor quadrado, então precisamos elevá-lo ao quadrado primeiro para obter o desvio padrão.

Para tornar o cálculo mais fácil, a fórmula da variância e do desvio padrão pode ser reduzida à fórmula abaixo.
Fórmulas de variante de dados
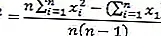
Fórmula de desvio padrão
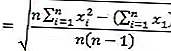
Observações :
s2 = variante
s = desvio padrão
x i = o iésimo valor de x
n = tamanho da amostra
Exemplo de problemas de desvio padrão
O seguinte é um exemplo e trabalho em problemas de desvio padrão.
Questão:
Sandi, como presidente dos membros extracurriculares, tem a tarefa de registrar a altura total dos membros. Os dados que a senha coletou são os seguintes:
167, 172, 170, 180, 160, 169, 170, 173, 165, 175
A partir dos dados acima, calcule o desvio padrão!
Leia também: Código Morse: História, Fórmulas e Métodos de MemorizaçãoResposta :
| Eu | x i | x i 2 |
| 1 | 167 | 27889 |
| 2 | 172 | 29584 |
| 3 | 170 | 28900 |
| 4 | 180 | 32400 |
| 5 | 160 | 25600 |
| 6 | 169 | 28561 |
| 7 | 170 | 28900 |
| 8 | 173 | 29929 |
| 9 | 165 | 27225 |
| 10 | 175 | 30625 |
| Σ | 1710 | 289613 |
A partir dos dados acima, pode-se ver que o número de dados (n) = 10 e graus de liberdade (n-1) = 9 também
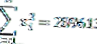
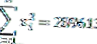
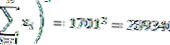
Para que possamos calcular o valor da variância da seguinte forma:

O valor variante dos dados coletados de Sandi é 30,32 . Para calcular o desvio padrão, só precisamos elevar o valor da variância ao quadrado para que:
s = √30,32 = 5,51
Portanto, o desvio padrão do problema acima é 5,51
Benefícios e aplicações
O desvio padrão é comumente usado por estatísticos para determinar se os dados obtidos são representativos de toda a população.

Por exemplo, alguém deseja saber o peso de uma criança de 3 a 4 anos em uma aldeia.
Então, para ficar mais fácil, precisamos apenas descobrir o peso de algumas crianças e depois calcular a média e o desvio padrão.
A partir dos valores de média e desvio padrão, podemos representar o peso corporal total de crianças de 3 a 4 anos em uma aldeia.
Referência
- Desvio Padrão - Fórmulas para Encontrar e Exemplos de Problemas
- Desvio Padrão: Fórmulas de Cálculo e Exemplos de Problemas
