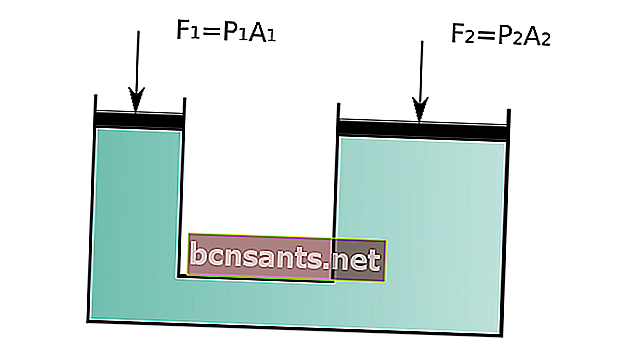
A lei de Pascal diz: "Se a pressão externa for aplicada a um sistema fechado, a pressão em qualquer ponto do fluido aumentará em proporção à pressão externa aplicada."
Você já viu quando uma oficina trocou pneus? Se for assim, certamente você verá que o carro ou mesmo o caminhão é içado primeiro com uma pequena ferramenta chamada macaco.
Claro que surge a questão de como um macaco pode levantar um carro que pesa até milhares de vezes do macaco.

A resposta a esta pergunta é explicada por uma lei chamada Lei de Pascal. Para obter mais detalhes, vamos examinar a Lei de Pascal junto com um exemplo do problema.
Compreendendo a Lei de Pascal
No século 16, um filósofo e cientista chamado Blaise Pascal cunhou uma lei chamada Lei de Pascal. Esta lei diz:
"Se a pressão externa for aplicada a um sistema fechado, a pressão em qualquer ponto do fluido aumentará em proporção à pressão aplicada externamente."
A ciência básica desta lei é a pressão, onde a pressão aplicada ao fluido com um sistema fechado será igual à pressão de saída do sistema.
Graças a ele, começaram a surgir inovações especialmente para resolver o problema de levantamento de cargas pesadas. Exemplos são macacos, bombas e sistemas hidráulicos de frenagem.
Fórmula
Antes de passarmos às equações ou fórmulas da Lei de Pascal, precisamos aprender a ciência básica, ou seja, a pressão. A definição de pressão em geral é o efeito ou a ação de uma força sobre uma superfície. A fórmula geral da equação é:
P = F / A
Onde :
P é pressão (Pa)
F é a força (N)
A é a área de superfície efetiva (m2)
A equação matemática da Lei de Pascal é muito simples, onde:
Leia também: Estrutura bacteriana, funções e imagens [COMPLETO]Entrar = Sair
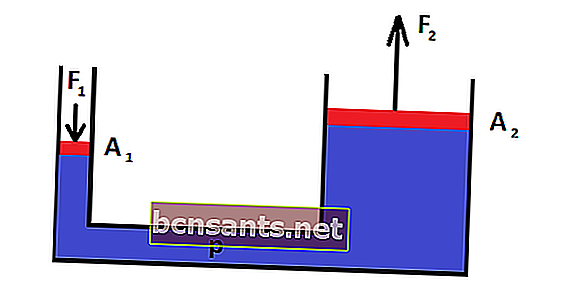
Com a figura acima, a equação da Lei de Pascal pode ser escrita como:
P1 = P2
F1 / A1 = F2 / A2
Com:
P1: pressão de entrada (Pa)
P2: pressão de saída (Pa)
F1: força aplicada (N)
F2: força produzida (N)
A1: área de força aplicada (m2)
A2: área resultante (m2)
Além disso, há outro termo usado na aplicação da Lei de Pascal, que é conhecido como vantagem mecânica. Em geral, a vantagem mecânica é a relação entre a força que um sistema pode produzir e a força que deve ser aplicada. Matematicamente, a vantagem mecânica pode ser escrita:
vantagem mecânica = F2 / F1
Como no exemplo do elevador hidráulico para carros, o fluido do sistema sempre terá o mesmo volume.

Portanto, a equação da Lei de Pascal também pode ser escrita como uma razão de volume de entrada e saída que:
V1 = V2
ou pode ser escrito como
A1.h1 = A2.h2
Onde :
V1 = volume empurrado
V2 = volume que sai
A1 = área da seção de entrada
A2 = sair da área seccional
h1 = profundidade da seção de entrada
h2 = altura da seção de saída
Exemplo de problemas
A seguir estão alguns exemplos e discussões de problemas com a aplicação da Lei de Pascal para que você possa entender mais facilmente.
Exemplo 1
Uma alavanca hidráulica é usada para levantar uma carga de 1 tonelada. Se a relação entre as áreas da seção transversal for de 1: 200, qual é a força mínima que deve ser aplicada na alavanca hidráulica?
Responda:
A1 / A2 = 1: 200
m = 1000 kg, então W = m. g = 1000. 10 = 10.000 N
F1 / A1 = F2 / A2
F1 / F2 = A1 / A2
F1 / 10000 = 1/200
F1 = 50N
Portanto, a força que o sistema tem que fazer é 50N
Exemplo 2
A vantagem mecânica de uma alavanca hidráulica tem um valor de 20. Se uma pessoa quiser levantar um carro de 879 kg, que força o sistema tem que fazer?
Responda:
m = 879kg, então W = mg = 879. 10 = 8790 N
ganho mecânico = 20
F2 / F1 = 20
8790 / F1 = 20
F1 = 439,5 N
portanto, a força exercida na alavanca é 439,5 N
Leia também: 1 ano Quantas semanas? (Anos a semanas) Aqui está a respostaExemplo 3
Uma alavanca hidráulica tem um diâmetro de pistão de entrada de 14 cm e um diâmetro de saída de 42 cm. Se o pistão desce a uma profundidade de 10 cm, qual é a altura do pistão que é levantado?
Responda:
O pistão tem uma superfície circular, então sua área é
A1 = π. r12 = 22/7. (14/2) 2 = 154 cm2
A2 = π. r22 = 22/7. (42/2) 2 = 1386 cm2
h1 = 10 cm
então
A1. h1 = A2. H2
154 10 = 1386. H2
h2 = 1540/1386
h2 = 1,11 cm
Portanto, o pistão que é levantado tem 1,11 cm de altura
Exemplo 4
Um compressor com uma mangueira ligada a uma torneira tem um diâmetro de 14 mm. Se um pulverizador com bico de 0,42 mm for instalado na extremidade da mangueira e quando o compressor for ligado, a pressão é medida em 10 bar. Determine a quantidade de força de exaustão de ar que sai do bico se a pressão do compressor não diminuir.
Resposta :
As mangueiras e orifícios têm uma área de seção transversal circular
Então a área da superfície do furo é
A2 = π. r22 = 22/7. (1,4 / 2) 2 = 1,54 mm2
"Lembre-se de que a Lei de Pascal explica que a pressão de entrada é igual à pressão de saída."
Para que a força aérea de saída seja:
P = F / A
F = P. UMA
F = 10 bar. 1,54 mm2
mude a barra de unidade para pascal e mm2 para m2
então
F = 106 Pa. 1,54 x 10-6 m2
F = 1,54 N
Portanto, a força do vento que sai é 1,54 N
Assim, a discussão sobre a Lei de Pascal, espero que possa ser útil para você.
