
Se você falar sobre fórmulas, e muito menos sobre física, sempre será contatado para memorizar questões. Basicamente, a fórmula não precisa ser memorizada, mas apenas compreendida. Agora vou ajudá-lo a não memorizar uma fórmula. Nem todas as dicas relacionadas ao processamento do cérebro para memorizá-lo, de forma alguma, meus amigos. Então, deixe-me apresentar a você, Dimensões de Magnitude!
Portanto, se você é um filho da física, certamente deve estar familiarizado com o nome Dimensão da Quantidade. Portanto, você saberá que existem 7 quantidades principais e suas unidades. Portanto, essas sete quantidades também têm suas dimensões. Então você pode ver mais abaixo.

E para algumas quantidades derivadas, as dimensões serão assim
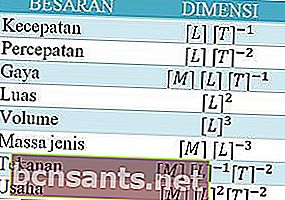
Então, o que isso tem a ver com não saber a fórmula?

Vou dar um exemplo. Suponha que você esqueceu a fórmula para o período de um pêndulo. O que você lembra é que ele tem um valor constante de 2 pi e tem algo a ver com o comprimento da corda e a aceleração da gravidade, então você acha que parece que a massa do pêndulo tem um efeito. Ok, então vamos começar.
Em primeiro lugar, você lista primeiro quais magnitudes afetam o período do pêndulo e, como mencionado acima,
- Comprimento da corda (l)
- Aceleração devido à gravidade (g)
- Massa do pêndulo (m)
Bem e agora fazemos a mágica. Para o período em si, a quantidade é o tempo, o comprimento da corda é o comprimento e a aceleração devido à gravidade, que é uma quantidade derivada que depende do comprimento e do tempo. Ok para a próxima, podemos fazer assim:
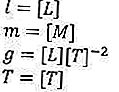
De qualquer forma, o conhecimento básico sobre expoentes também é muito necessário aqui, então é melhor antes de continuar, certifique-se de ter dominado os expoentes e não se esqueça da álgebra é claro.
Leia também: A fórmula para o perímetro de um triângulo (explicação, exemplos de perguntas e discussão)Agora então fazemos a equação assim
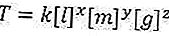
Então, por que existem variáveis? Sim, porque ainda não sabemos se a fórmula vai ser como, é por isso que damos uma variável lá. Então, por que não para T (ponto final)? Porque nós certamente sabemos que durante aquele período as unidades estão apenas segundos para uma posição, que tal isso. E para k em si, é uma constante que não afetará a solução mais tarde. Ok, claro que você pode entender, então procuramos o valor de cada variável
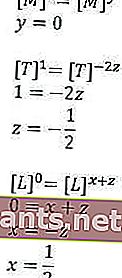
Para que possamos obter a fórmula substituindo os valores que foram obtidos
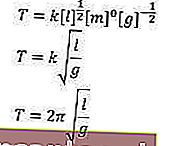
Sim, entendemos mano.

Bem, isso é o que geralmente é chamado de análise dimensional. A análise dimensional é muito útil para cientistas e engenheiros existentes fazerem cálculos precisos. Portanto, fiquem com vocês!
Esta postagem é a submissão do autor. Você também pode fazer sua própria escrita no Saintif juntando-se à Comunidade Saintif
Referência:
Giancoli, Douglas. 2014. Princípios de Física com Aplicações 7ª ed. Nova Jersey: PEARSON Prentice Hall
